Finding the equation of an ellipse using eccentricity and directrix with focus at (0,0)

Question

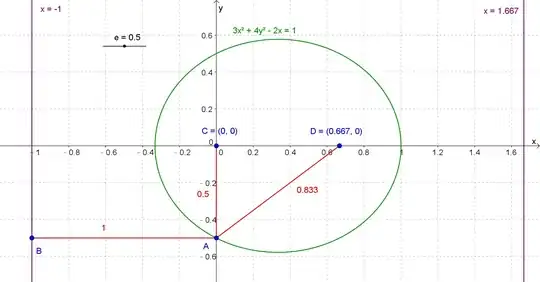
The ellipse $\varepsilon$ has eccentricty $\frac{1}{2}$, focus $(0,0)$ and the line $x=-1$ as the corresponding directrix. Find the equation of $\varepsilon$. Find the other focus and directrix of $\varepsilon$.

I'm confused by this due to fact the focus is at $(0,0)$. As far as I was aware the center of the ellipse should be at $(0,0)$ so that the foci are at $(c,0)$ and $(-c,0)$, where $c^2=a^2-b^2$. The directrix corresponding to the focus will then be given by the equation $x=\frac{a^2}{c}$, and the eccentricity of the ellipse is $\frac{c}{a}$. Is there another set of equations I can use to determine the equation of the ellipse?

Ng Chung Tak · Accepted Answer · 2016-11-19T17:58:24.490

2

From your information:

\begin{align*} \frac{\sqrt{x^2+y^2}}{x+1} &= \varepsilon \\ x^2+y^2 &= \varepsilon^2(x+1)^2 \\ (1-\varepsilon^2)x^2-2\varepsilon^2 x+y^2 &= \varepsilon^2 \\ \left[ (1-\varepsilon^2)x^2-2\varepsilon^2 x+ \frac{\varepsilon^4}{1-\varepsilon^2} \right]+ y^2 &= \varepsilon^2+\frac{\varepsilon^4}{1-\varepsilon^2} \\ \frac{(1-\varepsilon^2)^2}{\varepsilon^2} \left( x-\frac{\varepsilon^2}{1-\varepsilon^2} \right)^2+\frac{1-\varepsilon^2}{\varepsilon^2} y^2 &= 1 \\ a &= \frac{\varepsilon}{1-\varepsilon^2} \\ b &= \frac{\varepsilon}{\sqrt{1-\varepsilon^2}} \\ c &= \frac{\varepsilon^2}{1-\varepsilon^2} \end{align*}

The other focus is $$(2c,0)= \left( \frac{2\varepsilon^2}{1-\varepsilon^2},0 \right)$$

The other directrix is $$x=2c+1$$ $$x=\frac{1+\varepsilon^2}{1-\varepsilon^2}$$

edited Nov 19 '16 at 17:58

answered Nov 19 '16 at 14:07

Ng Chung Tak

18,990

I thought ellipses had equations of the form $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$? – math_apprentice Nov 19 '16 at 14:31
No, it's focus origin. In polar coordinates it reads $$r(\theta)=\frac{a(1-e^2)}{1-e\cos \theta}=\frac{b^2}{a-c\cos \theta}$$ See more for general form – Ng Chung Tak Nov 19 '16 at 14:34
Okay, thanks. I'm not sure I understand. What is the equation of the ellipse? Is $\varepsilon$ in your equation $\frac{1}{2}$? If I substitute that in will I get the equation of the ellipse? – math_apprentice Nov 19 '16 at 14:38
Yes, of course. – Ng Chung Tak Nov 19 '16 at 14:39
Okay, I will try that. Thanks. – math_apprentice Nov 19 '16 at 14:41
Correct some mistakes. – Ng Chung Tak Nov 19 '16 at 17:25
Let us continue this discussion in chat. – math_apprentice Nov 19 '16 at 17:44

Finding the equation of an ellipse using eccentricity and directrix with focus at (0,0)

1 Answers1