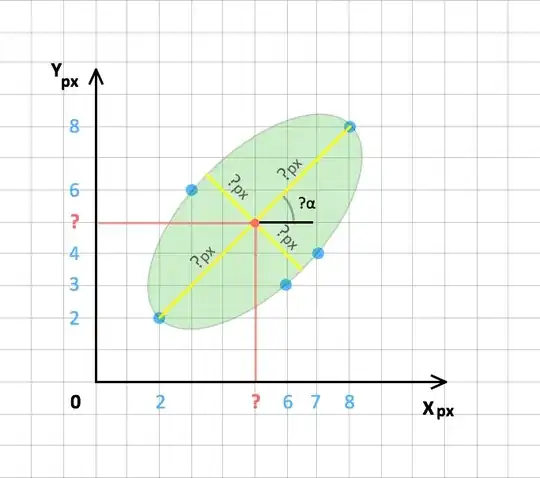
I create an algorithm recognizing ellipses in images.
I have five coordinates (points) possible ellipse.
(8.8) (7.4) (6.3) (3.6) and (2.2)
I use the formula of the conical section of the second order:
$Ax ^ 2 + Bxy + Cy ^ 2 + Dx + Ey + F = 0$
And determines the type of conic section by the value of the discriminant.
$B ^ 2-4AC$
Where, if the sign of the value < 0, then this ellipse.
On the basis of the coordinate values I find A, B, C, D, E, F. (Calculates them here)
A = 0.0763889
B = -0.0902778
C = 0.0763889
D = -0.312500
E = -0.312500
F = 1.00000
But I do not know what to do next calculations.
How do I need to get the coordinates of the center of the ellipse, the length of its two axes, and rotation about the coordinate axes?
Thank you!