Finding angle of rotation $\theta$ that transforms a standard ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ into $2x^2+2xy+2y^2-5=0$

Question

The ellipse with equation $2x^2+2xy+2y^2-5=0$ is obtained from the standard ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ by rotating through angle $\theta$.

Determine the angle of rotation $\theta$.

I used the standard method of the coefficient of $xy$~ (can't get ~ signs) being $0$. I worked out $\theta = \frac{\pi}{4}$.

Is this the correct angle of rotation ?

You can check that yourself if you set up the matrix for rotation by $\pi/4$ and applying it to the standard ellipse you mention. However one would need the values of $a,b$ as these do not appear in your goal ellipse. — coffeemath, Apr 17 '23 at 18:17
@coffeemath Yes I did I think it’s right but I wanted to make sure it is — , Apr 17 '23 at 18:57
My suggestion is that you include the rotation matrix you found in your question, along with the steps you took using it which made you think it's correct. That way someone can check your work. Otherwise no one can. — coffeemath, Apr 17 '23 at 19:05
I can't find my analytic geometry lecture notes... There was a formula. — Bob Dobbs, Apr 18 '23 at 11:50
The rotation angle depends on the initial position of the ellipse: if the long axis is vertical (your finding of $a^2, b^2$) then the rotation is $\frac \pi4$; otherwise, of the long axis is horizontal then the rotation is $-\frac \pi4$. — WindSoul, Apr 18 '23 at 12:03
Both ellipses share center $(0,0)$, then it is center of rotation. $2x^2+2xy+2y^2-5=0$, $x^2+y^2=5-(x+y)^2 \leq 5$, then farthest points of ellipse are such that $x^2+y^2=5$, $x+y=0$. One of these points is $x=\frac{\sqrt{5}}{\sqrt{2}}$, $y=-\frac{\sqrt{5}}{\sqrt{2}}$. Polar angle of this point is $-\frac{\pi}{4}$. This point can be obtained from one of points $(a,0)$, $(0,b)$, $(-a,0)$, $(0,-b)$ having polar angles $0$, $\pi/2$, $\pi$, $-\pi/2$. Then possible angles of rotation are $-\pi/4$, $-3\pi/4$, $3\pi/4$, $\pi/4$. — Ivan Kaznacheyeu, Apr 18 '23 at 12:08
$\tan2\theta=\frac{b}{c-a}=\pm\infty\implies \theta=\pm\frac{\pi}{4}$. It is so easy. Maybe the reason of downvotes... :( — Bob Dobbs, Apr 18 '23 at 13:44
@BobDobbs Please check my working in my official answer below. — , Apr 18 '23 at 16:27
@BobDobbs Can I choose either the positive or negative value then ? — , Apr 18 '23 at 16:27
@NikitaMazepin I think two of them is enough... Is the verb "to subb" accepted in math community? I will use it. — Bob Dobbs, Apr 18 '23 at 16:58
@NikitaMazepin For determining the possible pairs $(a,b)$... — Bob Dobbs, Apr 18 '23 at 17:01

score 1 · Answer 1 · edited May 16 '23 at 01:40

1

My working. I can solve $\cot(2 \theta) = \frac{A-C}{B} = 0$, so $2\theta = \frac{\pi}{2} + k \pi$, so $\theta = \frac{\pi}{4} + \frac{k \pi}{2}$. Does that mean any angles of this form work ? I choose $\theta = \frac{\pi}{4}$.

Transformation: $x = X \cos(\theta) - Y\sin(\theta)$ and $y = X\sin(\theta)+Y\cos(\theta)$.

I subbed this in to obtain $\frac{X^2}{5/3} + \frac{Y^2}{5} = 1$

edited May 16 '23 at 01:40

Gary

31,845

answered Apr 18 '23 at 16:27

Why are A and C capital but b is small? – Bob Dobbs Apr 18 '23 at 17:00
@BobDobbs Edit made now, thanks – Apr 18 '23 at 17:00
For $k=0, \theta=\frac \pi4$ and you got the right result: vertical ellipse rotated $\frac \pi4$. However, for $k=1, \theta=\frac{3\pi}4$ the values of $a^2, b^2$ swap and the original ellipse has horizontal long axis. – WindSoul Apr 18 '23 at 17:18
@WindSoul Ohhh, I think I understand. So you are saying the major and minor axis switch basically – Apr 18 '23 at 17:24
@WindSoul Say if a question says they want the ellipse to have a horizontal long axis, is there a way of knowing whether to choose $\frac{\pi}{4}$ or $\frac{3\pi}{4}$? And those are the only two relevant ones right ? – Apr 18 '23 at 17:35
1

Yes: the axes are switching depending on rotation angle. A rotation of $\frac{3\pi}4$needs applied to an ellipse with horizontal long axis. If you plug $\frac{3\pi}4$ in the boxed formula you could see $a^2\gt b^2$: horizontal long axis. If you plug in $\frac \pi4$ in the boxed formula you could see $a^2\lt b^2$ therefore the long axis is vertical. – WindSoul Apr 18 '23 at 18:02
@WindSoul thank you. You answered my question. My original confusion was that there infinite possible angles. So half of them give the same ellipse as each other, but the two groups have different major axis basically – Apr 18 '23 at 18:21
1

There is still some ambiguity to deal with. The rotated ellipse came off a standard position. The standard position of and ellipse is centered in origin and with long axis (of simmetry) horizontal. In this case there is one principal angle of rotation: $\frac {3\pi}4$. Principal angle is positive less than $2\pi$. – WindSoul Apr 18 '23 at 18:37
What about $\frac{\pi}{4}? Isn’t that a principal angle of rotation too ? – Apr 18 '23 at 19:38
1

The standard equation of an ellipse $\frac {x^2}{a^2}+\frac{y^2}{b^2}=1$ assumes the ellipse is centered at origin and the long axis is horizontal, thus $a\gt b$. For this reason only $\frac {3\pi}4$ would be a principal angle of rotation. Regarding $\frac \pi4, \frac {5\pi}4$, while they are still principal angles of rotation, they do not relate to the standard equation because for those angles a<b meaning the ellipse is not in standard position, with the long axis horizontal. – WindSoul Apr 19 '23 at 10:21

WindSoul · Accepted Answer · 2023-04-18T18:41:46.577

This is how the rotated ellipse looks like, according to Desmos:

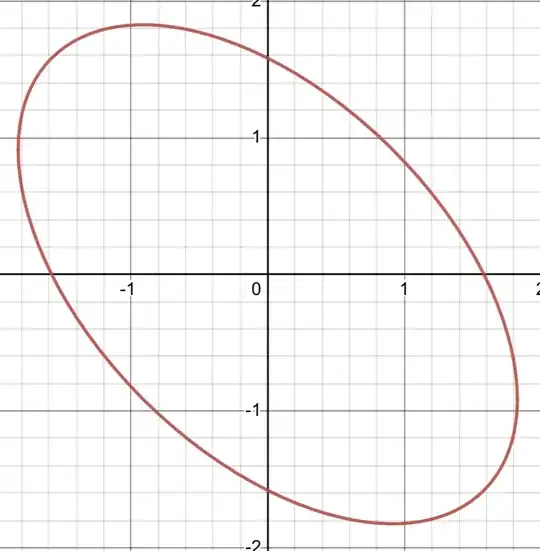
Apparently the ellipse is rotated by $-\frac \pi4$, if the long axis was horizontal. However, if the long axis was vertical then the ellipse is rotated by $\frac \pi4$.

The coordinates of a point on the rotated ellipse are $$(x_r,y_r)=(x\cos \theta-y\sin \theta,x\sin \theta+y\cos \theta)$$

The given equation of the rotated ellipse is: $$\begin{align}&2x^2_r+2y^2_r+2x_ry_r=5\\ &\Leftrightarrow 2(x\cos \theta-y\sin \theta)^2+2(x\sin \theta+y\cos \theta)^2+2(x\cos \theta-y\sin \theta)(x\sin \theta+y\cos \theta)=5\\&\Leftrightarrow 2x^2(1+\cos \theta\sin\theta)+2y^2(1-\cos \theta \sin\theta)+2xy\underbrace{(\cos^2\theta-\sin^2\theta)}_{=0}=5\\&\Leftrightarrow\boxed{\frac{x^2}{\frac 5{2(1+\frac{\sin 2\theta}2)}}+ \frac{y^2}{\frac 5{2(1-\frac{\sin 2\theta}2)}}=1, \cos^2\theta=\sin^2\theta}\end{align}$$

Two solutions are possible depending on the solution of $\cos^2\theta=\sin^2\theta$:

$$\begin{align}\cos^2\theta=\sin^2\theta&\Rightarrow \cos\theta=\sin\theta\\&\Rightarrow \theta=\frac \pi4+k\pi, k\in \Bbb Z\\&\Rightarrow a^2=\frac 53, b^2=5\text{ : long axis is vertical}\end{align}$$

I would not consider an ellipse with long axis vertical because the rotation is presumed to come off a standard position where the original ellipse was centered in origin with the long axis horizontal.

$$\begin{align}\cos^2\theta=\sin^2\theta&\Rightarrow \cos\theta=-\sin\theta\\&\Rightarrow \theta=\frac {3\pi}4+k\pi, k\in \Bbb Z\\&\Rightarrow a^2=5, b^2=\frac 53\text{ : long axis is horizontal}\end{align}$$

Solving $\cos^2\theta=\sin^2\theta$ leads to finding $a^2,b^2$, thus telling wether the initial ellipse was with long axis horizontal ($\cos^2\theta=-\sin^2\theta$) and rotated $-\frac\pi4$or vertical ($\cos^2\theta=\sin^2\theta$) and rotated $\frac \pi4$. — WindSoul, Apr 18 '23 at 17:11

Finding angle of rotation $\theta$ that transforms a standard ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ into $2x^2+2xy+2y^2-5=0$

2 Answers2

Linked