Is there any geometric way to characterize $e$?

Question

Let me explain it better: after this question, I've been looking for a way to put famous constants in the real line in a geometrical way -- just for fun. Putting $\sqrt2$ is really easy: constructing a $45^\circ$-$90^\circ$-$45^\circ$ triangle with unitary sides will make me have an idea of what $\sqrt2$ is. Extending this to $\sqrt5$, $\sqrt{13}$, and other algebraic numbers is easy using Trigonometry; however, it turned difficult working with some transcendental constants. Constructing $\pi$ is easy using circumferences; but I couldn't figure out how I should work with $e$. Looking at

made me realize that $e$ is the point $\omega$ such that $\displaystyle\int_1^{\omega}\frac{1}{x}dx = 1$. However, I don't have any other ideas. And I keep asking myself:

Is there any way to "see" $e$ geometrically? And more: is it true that one can build any real number geometrically? Any help will be appreciated. Thanks.

Answer 1

For a certain definition of "geometrically," the answer is that this is an open problem. You can construct $\pi$ geometrically in terms of the circumference of the unit circle. This is a certain integral of a "nice" function over a "nice" domain; formalizing this idea leads to the notion of a period in algebraic geometry. $\pi$, as well as any algebraic number, is a period.

It is an open problem whether $e$ is a period. According to Wikipedia, the answer is expected to be no.

In general, for a reasonable definition of "geometrically" you should only be able to construct computable numbers, of which there are countably many. Since the reals are uncountable, most real numbers cannot be constructed "geometrically."

Answer 2

The area beneath the reciprocal function $$x\mapsto\frac{1}{x}$$ from $x=1$ to $x=e$ is $1$. Though this isn't really geometric like you want, it is still a clear way to see $e$ physically.

Answer 3

Debeaune asked Descartes this problem in a letter in 1638:

Consider a curve $y=f(x)$. Lets consider the tangent line $t(x)$ through the point $(x_{0},y_{0})$ which would look like $t(x) = y_{0} + f'(x_{0})\cdot(x-x_{0})$. What curve has the property that, every such tangent line intersects the $x$ axis at $x_{0}-1$, i.e., $$ t(x_{0}-1)=0 $$ What curve can do this? Only $y=C\exp(x)$...where $C$ is some nonzero constant.

For a thorough derivation, see http://pqnelson.wordpress.com/2012/06/03/exponential-function/

Answer 4

You can't build any real number geometrically. They aren't even all computable. If you don't want to consider functions, you could (this is kind of cheating) look at $\lim_{n\rightarrow\infty} (1+\frac 1 n)^n$ as the volume of a suitably sized hypercube as the dimension increases.

Answer 5

I'll take my comment at the answer of Alex Nelson and make it into a separate answer, although it is really just the same answer reformulated. But I'll start pre-empting the predictable comment "I would call this a way of recognizing $e$, not constructing $e$" by countering that, even if one proclaims that constructing a point at a given distance along a curved line is a valid operation, one still cannot construct $\pi$ with ruler and compass either: one can only recognise it as the distance around a circle of diameter $1$ needed to get to the point diametrically opposite to the starting point.

Obviously we need some non-ruler-and-compass ingredient to construct $e$. I'll take this to be the graph of some exponential function, together with its unique asymptote: say in some coordinate system in which that asymptote is the $x$-axis we are given the set of points $(x,a^x)$ for some $a>1$ (neither the unit length of the coordinate system nor the value of $a$ need to be known; the $x$-axis is of course determined by the graph, but I'd have difficulty giving a construction of it).

Here is the construction: pick a point $P$ on the graph, find the point of intersection $Q_0$ of the tangent line to the graph at $P$ with the $x$-axis. Then taking perpendiculars to the $x$-axis through $P$ and $Q_0$ which intersect the $x$-axis in $P_0$ respectively the graph in $Q$, one has $\frac{PP_0}{QQ_0}=e$.

Answer 6

Another approach might be finding a polar curve such that its tangent line forms a constant angle with the segment from $(0,0)$ to $(\theta,\rho(\theta))$. The solution is the logarithmic spiral, defined by

$$\rho =c_0 e^{a\theta}$$

Answer 7

Plot the curves $y = a^x$ for $a > 0$. As $a$ gets larger, you find the slope of the tangent line is larger. If $a < 1$, this slope is negative. There is exactly one value for which the slope is 1, and that is $e$.

You can use this to define $e$ and derive the fact that $e=\sum_{n\ge 0}1/n!$.

Answer 8

The answer is "yes, you can," if you think beyond Euclidean geometry and consider geometric quantities appearing in hyperbolic geometry. In the Euclidean geometry, the number $\pi$, of course, you "see" by looking at circumferences and areas of circles. In hyperbolic geometry, the circumference of the circle of radius $r$ is $$ L_h(r)= 2\pi \sinh(r), $$ see for instance here.

Hence, for the unit circle, we get $$ L_h(1)= \pi\left(e - \frac{1}{e}\right).$$ This gives you a mixture of $e$ and $\pi$. In order to "see" $e$ by itself, we can look at the ratio of hyperbolic lengths: $$ \frac{L_h(r+1)}{L_h(r)}= \frac{\sinh(r+1)}{\sinh(r)}. $$ We got rid of $\pi$ but did not get $e$ (yet). To get $e$, you look at the asymptotics of this ratio as $r\to \infty$. In the Euclidean case, we would get $$ \lim_{r\to\infty} \frac{2\pi (r+1)}{2\pi r}= 1 $$ (another universal constant), while in the hyperbolic case, the limit is $$ \lim_{r\to\infty} \frac{\sinh(r+1)}{\sinh(r)}= \lim_{r\to\infty} \frac{e^{r+1} - e^{-(r+1)}}{e^r - e^{-r}}= e. $$ If you do not regard limits as geometric operations (I do think of limits geometrically), then instead think of this as the supremum $$ \sup_{r\ge 1} \frac{L_h(r+1)}{L_h(r)}= e. $$

This is how to "see" $e$ geometrically.

Incidentally, there are many ways to "see" $\pi$ in hyperbolic geometry. My favorite is that $\pi$ is the supremum of areas of hyperbolic triangles. The bottom line is that you can "see" more in hyperbolic geometry than in Euclidean geometry.

Answer 9

From a geometrical viewpoint, Euler's constant $e$ is equal to the sum of the volume of all standard $d$-simplexes, i.e. over all positive integers $d$.

Alternatively, one can states that $e$ is equal to the sum of the first hyperoctant hypervolume of all $d$-dimensional hypertetrahedrons with standard unit vectors as vertices, i.e. over all non-negative integers $d$.

Answer 10

There is another fomulation of Euler’s Number that is geometric in nature (using hypercubes):

Here is Euler's Number expressed a series of hypercubes each divided by n!, where n is the dimension of the hypercube.

$$e^{x} = \sum_{n=0}^{\infty} \frac{x^{k}}{k!} = \frac{x^{0}}{0!} + \frac{x^{1}}{1!} + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + \frac{x^{4}}{4!} + \cdots $$

You'll notice a similarity to elementary problems in combinatorics: from an arbitrary set {a,b,c,d,e} where each element is in [0,x], how many ways can you form coordinates in $\mathbb{R}$³? It's just a combination with repetition problem. There are

$$\binom{n + 1 - r}{r}$$

such ways. Similarly, each term can be thought of the set of combinations of coordinates with repetition in each hypercube space.

Answer 11

Here is another way to "see" (not construct) $e$ geometrically.

In a semicircle, draw zigzag line segments that, together with the base, form $n$ equal-width isosceles triangles whose top vertices lie on the semicircle. Here is an example with $n=6$.

$e$ is the diameter of the semicircle such that the product of the lengths of the line segments converges to a positive number as $n\to\infty$.

The limit can be expressed as $\lim\limits_{n\to\infty}\prod\limits_{k=1}^n e^2\left(\left(\frac{1}{2n}\right)^2+\frac14-\left(\frac{k}{n}-\frac{1}{2n}-\frac12\right)^2\right)$, which turns out to equal $2$.

Answer 12

Don't knowing if this answer could met your expectatives, but I have made a similar question here, and so far I have found this:

Through the properties $\lim_{x \to 0} (1+x)^{\frac{1}{x}} = e$ and $\lim_{x \to 1} (1+x)^{\frac{1}{x}}= 2$, and using that $\log(1+x)=\int_1^{1+x} \frac{du}{u}$, you could use:

$$\int_0^1 \frac{\partial}{\partial x}\left[2x-(1+x)^{\frac{1}{x}} \right]\,dx = e$$ $$ \iff \int\limits_0^1 \left(2-(1+x)^{\frac{1}{x}}\left(\frac{1}{x(1+x)}-\frac{\log(1+x)}{x^2}\right)\right) \,dx = e$$

where the constant $e$ is not explicetly involved, but its hidden that it still requires to find the limit $\lim_{x \to 0} (1+x)^{\frac{1}{x}} = e$ so I don't know if its valid (under the integral is just a point of zero meassure, so maybe the problem is avoided, but I don't really know), but I found it interesting enough to be shared, maybe someone gets an idea to improve it.

It is possible to use also terms of the form $q(x)=\left(1+\tan\left(\frac{\pi x}{2}\right)\right)^{\cot\left(\frac{\pi x}{2}\right)}$ to find that $$\int_0^1 1-q'(x)\ dx=e$$ but is almost the same function but even more complicated, and also has the same limitations due the logarithm appearing on the derivative.

Another related ones: $$\int_0^1 \frac{\partial}{\partial x}\left[2x+(2-x)^{\frac{1}{1-x}} \right]\,dx = e$$

$$\int_0^1 \frac{\partial}{\partial x}\left[2x+\frac{1}{2}\left((2-x)^{\frac{1}{1-x}}-(1+x)^{\frac{1}{x}}\right) \right]\,dx = e$$

So at least the area below these functions adds up to $e$.

Answer 13

From the hyperbolic identity:

          cosh(x) + sinh(x) = e^x  ...in general,

we have

          cosh(2) + sinh(2) = e^2  ...in particular.

If we take individually, the square of the square root of each of the first two terms of the second equation, we have a Pythagorean identity, where the sides are:

F = √(cosh(2)), G = √(sinh(2)), and the hypotenuse of the right-angled triangle, H = e.

I hear you say, not as good as π, the ratio of the circumference of a circle to its diameter, since one can measure the circumference and the diameter, by some means. One needs the formula or Taylor series for cosh(2) and sinh(2).

(My original edit here was pointless. It involved the additional identity:

         1  +  sinh^2(x)  =  cosh^2(x)

which is also a Pythagorean identity, but since it can be derived from the previous case, and vice versa, it was pointless in calculating a value for 'e').

N.B. 'e', the base of natural logarithms, was created as a valid idea in calculus, to make differentiation, and therefore integration, easier. It is not a geometrical constant, but a mathematical constant, and is the limit of:

                      (1 + t)^(1/t), as t tends to 0

which occurs in the differentiation of log(x).

Answer 14

EDIT: To my answer (under the line) I am gonna add pictures I have draw- I construct an aprroximation of $e$ into 5th iteration on the Number Line, where:

$$L_0=a_0=1 $$ $$L_{n+1}=L_n+a_{n+1} ; a_{n+1}=\frac{a_n}{n+1} $$

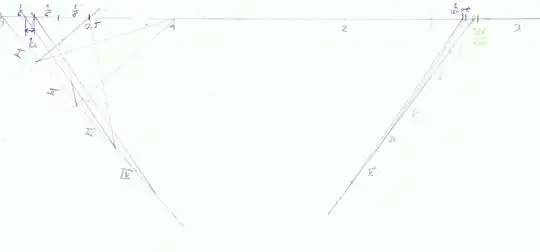Altenative we can write:

$$L_2=2.5 ;a_2=0.5 $$ $$L_{n+1}=L_n+a_{n+1} ; a_{n+1}=\frac{a_n}{n+1} $$

Here I tried to approximate between $[2;3]$ (into 6th step):

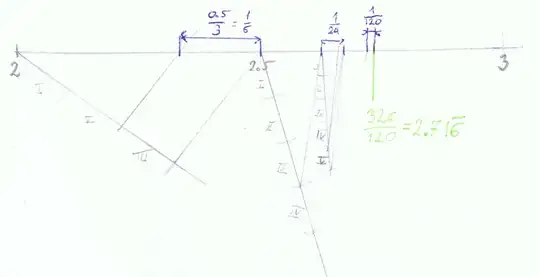
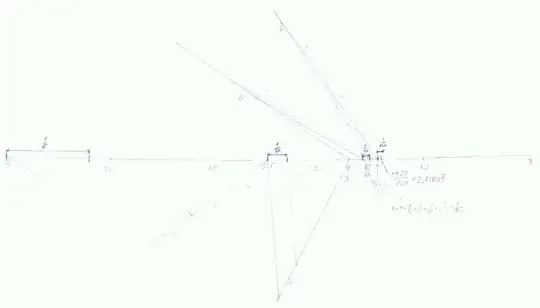
Old Answer:

---Introduction---

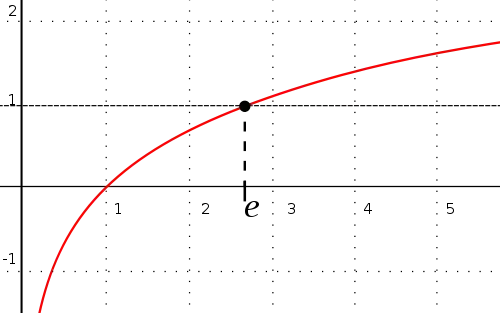
A) We gonna use the Taylor series for $e$ and multiply by $A$:

$e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+...=1+\frac{1}{1}+\frac{1}{1*2}+\frac{1}{1*2*3}+\frac{1}{1*2*3*4}+...$

$Ae=A(1+\frac{1}{1}+\frac{1}{1*2}+\frac{1}{1*2*3}+\frac{1}{1*2*3*4}+...)$

In special case: $A=1$ (leght unit)

We can lead $Ae$ to this form:

$Ae=A(1+\frac{1}{1}(1+\frac{1}{2}(1+\frac{1}{3}(1+\frac{1}{4}(1+...)...)...)$ (Formula 1)

B) Optional: How a line segment can be devide via ruler and compass: Intercept theorem

C) (Formula 1) will be explained as an Algorithm plus picture .

---The Algorithm---

Short :

Start:

• Have a line segment $a_0$ with a length of $A$ .

Loops:

I) Duplicate $a_{n-1}$ and divide the new segment into $n$ equal parts. Pick one element as $a_n$.

II) Add $a_{n-1}$ to the older line segments: $L_{n-1}=a_{n-1}+\displaystyle\sum_{i=0}^{n-2}a_i$

Long :

1. Have a line segment $a_0$ with a length of $A$ .

1.1. Duplicate $a_0$ and divide the new segment into $1$ equal parts .

1.2. Pick one element as $a_1$.

1.3. Add $a_0$ to the older line segments: $L_0=a_0$

2.1. Duplicate $a_1$ and divide the new segment into $2$ equal parts .

2.2. Pick one element as $a_2$.

2.3. Add $a_0$ to the older line segments: $L_1=a_1+a_0$

3.1. Duplicate $a_2$ and divide the new segment into $3$ equal parts .

3.2. Pick one element as $a_3$.

3.3. Add $a_2$ to the older line segments: $L_2=a_2+a_1+a_0$

.

.

.

n.1. Duplicate $a_{n-1}$ and divide the new segment into $n$ equal parts .

n.2. Pick one element as $a_n$.

n.3. Add $a_{n-1}$ to the older line segments: $L_{n-1}=a_{n-1}+(a_{n-2}+...+a_2+a_1+a_0)$

---Picture---