19

I was solving a question :

Let $x_1=1$ and $x_{n+1} = \sqrt{1+x^2_n } \ \ \forall \ \ n\in \mathbb{N}$

Then evaluate $$\lim_{n \to \infty} \left( \frac{x_{n+1}}{x_n} \right)^n$$

The way I did it was :

$$x_1^2=1$$

$$x_2^2=2$$

$$x_3^2=3$$

$$x_4^2=4$$

$$x_{n+1}^2=(n+1)$$

$$\therefore \lim_{n \to \infty} \left( \frac{x_{n+1}^2}{x_n^2} \right)^\frac{n}{2}$$

$$A = \lim_{n \to \infty} \left( \frac{n+1}{n} \right)^{\frac{n}{2}}$$

$$\ln(A) = \lim_{n \to \infty} \frac{1}{2} \frac{\ln\left( 1+ \frac{1}{n} \right)}{\frac{1}{n}} $$

Applying L'Hopital's rule :

$$\ln(A) = \frac{1}{2}$$

$$A = \sqrt{e}$$

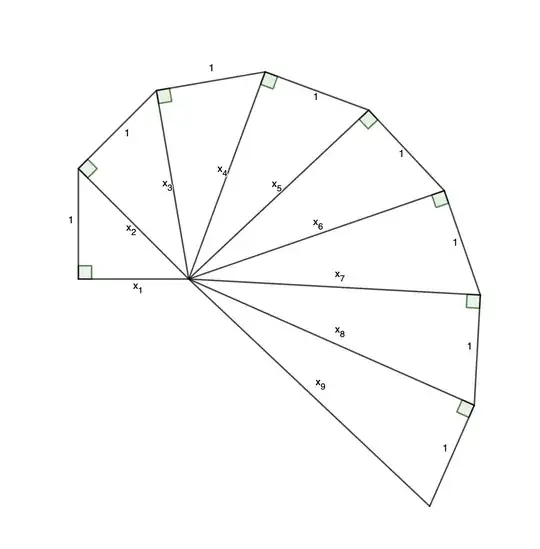
But what I think is that this could also be solved using a geometric approach. I believe so because the recurrence relation given is similar to the Pythagoras Theorem.

$$x_{n+1}^2 = 1^2 + x_n^2$$

I tried to draw the diagram for something like this :

enter image description here

However all I could conclude was the indeterminate form the was forming :

For the the limit is of the secant of the base angle of the triangle ( $(\sec \alpha)^n$) with $x_n$ as the base.

i.e. the limit becomes :

$$\lim_{n \to \infty} \sec^n (\alpha_n)$$

which I can see that as $n$ approaches $\infty$, $\alpha_n$ will keep decreasing until we can say $x_n \approx x_{n+1}$, so it is a $(1)^\infty$ form.

So my question is :

How would one prove the above question using geometry?

The Dragonborn
  • 348
  • That 's a neat way to interpret the expression in the limit. The angle of the secant though depends on $n$, that is you have $\sec^n(\alpha_n)$. I can't say that the geometric intuition will sill you and answer to how $\alpha_n$ changes, but the evaluation of the limit (in hindsight) does. – Mittens Jun 18 '20 at 18:59
  • 3
    It would be the very first occurence of $e$ in Euklidean geometry, as far as i know: –  Jun 18 '20 at 19:06
  • 1
    @ProfessorVector idk if this is purely Euclidean geometry, as we are also invoking some calculus. – The Dragonborn Jun 18 '20 at 19:08
  • https://math.stackexchange.com/questions/159707/is-there-any-geometric-way-to-characterize-e – pisoir Feb 13 '21 at 18:41

1 Answers1

1

You can define as $\alpha_n$ the angle of the Pythagorean triplet $(1, x_n, x_{n+1})$ between the sides of length $x_n$ and $x_{n+1}$. Its value comes from $$ \tan\alpha_n = \frac{\sin\alpha_n}{\cos\alpha_n} = \frac{1/x_{n+1}}{x_n/x_{n+1}} \implies \alpha_n = \cot^{-1} x_n. $$

From your drawing, one can see (as you suggested) that $$ \frac{x_{n+1}}{x_n} = \sec\alpha_n = \sec\cot^{-1}x_n = \sqrt{\frac{x_n^2+1}{x_n^2}} = \sqrt{\frac{n+1}{n}}. $$

Therefore, $$ \boxed{\lim_{n \rightarrow +\infty} \left( \frac{x_{n+1}}{x_n} \right)^n = \lim_{n \rightarrow +\infty} \left( 1 + \frac{1}{n} \right)^{n/2} = \sqrt{e}.} $$

Sebastián V. Romero
  • 518