2

I never really understood what $e$ means and I'm always terrified when I see it in equations. What is it? Can somebody dumb it down for me? I know it's a constant. Is it as simple as that?

Thomas Russell
  • 10,425
  • 5
  • 38
  • 66
Gannicus
  • 341
  • 1
    Are you familiar with calculus? – Dan Rust May 14 '13 at 16:19
  • 3
    To scare you a bit more: it's (probably) the most important constant in all of mathematics. To perhaps scare you a bit less: take any calculator and try $1.01^{100}$, $1.001^{1000}$, and so on, and see what answer you start approximating. – snar May 14 '13 at 16:19
  • This thread may help a bit: http://math.stackexchange.com/questions/387746/pi-from-the-unit-circle-sqrt-2-from-the-unit-square-but-what-about-e – Jared May 14 '13 at 16:21
  • If you just see something like $x = e + 1$, then just remember that $e$ approximately equals $2.718$. So under these premises, $x$ approximately equals $3.718$. If you see something more like $y = e^x + 1$, then that requires a bit more explanation. – goblin GONE May 14 '13 at 16:21
  • @Daniel Yes. I know it sounds dumb but I'm now studying Analytic Calculus but never understood the idea of 'e' entirely. – Gannicus May 14 '13 at 16:22
  • 2
    I would say you should be more interested in the function $e^x$ than the constant $e$... – J. M. ain't a mathematician May 14 '13 at 16:32
  • @J.M. And that function should better be called $\exp(x)$ than $e^x$. – Hagen von Eitzen May 14 '13 at 16:33
  • @Hagen, I prefer writing $\exp(x)$ too, but I thought introducing that notation is best left to a nicely expository answer... – J. M. ain't a mathematician May 14 '13 at 16:35
  • possible duplicate of Intuitive Understanding of the constant "e". Also related: http://math.stackexchange.com/questions/159707/is-there-any-geometric-way-to-characterize-e http://math.stackexchange.com/questions/308462/is-there-a-simple-geometrical-description-of-e http://math.stackexchange.com/questions/272507/how-would-you-explain-why-e-is-important-and-when-it-applies – MJD May 14 '13 at 16:42
  • Think of it as a pimped-up $2$. – k.stm May 14 '13 at 16:44

5 Answers5

7

Euler's Number, $e\approx2.718281828$, is a special constant in calculus because of several important properties it holds.

First, $y=e^{x}$ (also written as $y=\exp(x)$ due to the exponential growth of the function) and constant multiples thereof is the only function for which:

$$\frac{dy}{dx}=y$$

Which means in simple language that the gradient of the curve at a point is proportional to the value of the curve at that point. For instance, at the point $(1,e)$, the gradient of the tangent (shown as blue in the graph below) to the curve $y=e^{x}$ (shown in red) is $e$.

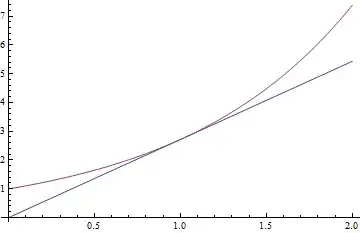
                                     Graph showing tangent to the exponential curve at (1,e)

A proof that $y=C\exp(x)$ is the only real function for which this rule applies can be found here.

Euler's Number is also the number which the expression $\left(1+\frac{1}{x}\right)^{x}$ approaches as $x$ gets closer and closer to infinity. Formally:

$$\lim_{x\to\infty}\left(1+\frac{1}{x}\right)^{x}=e$$

Euler's number also can be found as the unique positive real number $e$, such that:

$$\int_{1}^{e}\frac{dt}{t}=1$$

Which in common language means the area under the curve $y=\frac{1}{x}$ between $1$ and $e$ has unit area (or area equal to 1).

Also, interestingly, $e$ can be found by applying Stirling's approximation to the factorial in reverse to get:

$$e=\lim_{n\to\infty}\frac{n}{\sqrt[n]{n!}}$$

Community
  • 1
Thomas Russell
  • 10,425
  • 5
  • 38
  • 66
3

$e$, the constant, is the limit of $(1 + {1\over n})^n$ as n approaches infinity; As expressed by the series: $$e = 1 + {1\over 1} + {1\over 1\cdot2 } + {1\over 1\cdot2\cdot3} + {1\over 1\cdot2\cdot3\cdot4} + ... + {1\over 1\cdot 2\cdot...\cdot\infty}$$

It is the base of the natural logarithm.

JohnWO
  • 2,089
  • 14
  • 29
2

The idea of $e$ may be explained through the concept of compound interest. Let's say that you earn an annual interest rate $r$ on a principal $P$ dollars. Let's say that the money is compounded annually. Then after $n$ compounding periods, you have $P (1+r)^n$ dollars.

Now lets say we compound semiannually; then after the same amount of time $n$ years, i.e., $2 n$ compounding periods, you will have

$$P \left ( 1+\frac{r}{2} \right )^{2 n}$$

dollars. You can now imagine more frequent compounding events; let's say that there are $M$ such events per year. Then after $n$ years you will have

$$P \left ( 1+\frac{r}{M} \right )^{M n}$$

dollars.

Now imagine that you are compounding continuously (like, every microsecond). This corresponds to the limit as $M \to \infty$: after $n$ years, you will have

$$P \lim_{M \to \infty} \left ( 1+\frac{r}{M} \right )^{M n} =P\, e^{r n}$$

dollars.

Ron Gordon
  • 138,521
1

The simplest way to understand it is, consider the following equation:

$$f(x)=\left(1+\frac{1}{x}\right)^x$$

As $x$ gets larger and larger, notice what number it gets closer to:

$$f(1)=2$$ $$f(2)=2.25$$ $$f(3)\approx 2.37073$$ $$...$$ $$f(1000)\approx 2.7169$$ $$...$$

It is important in mathematics because it is arguably the single real number most commonly found in nature (from heat flow to battery discharge to population growth/decay models), which is why its inverse is called the natural logarithm.

G Tony Jacobs
  • 31,218
rurouniwallace
  • 6,266
1

On can show that there are functions $f(x)$ with the property $$\tag1f'(x)=f(x)$$ for all $x$. If one additionally requires $f(0)=1$, the solution is unique and called $\exp(x)$. From this property alone, it follows that the general solution to $f'(x)=f(x)$ is $f(x)=c\exp(x)$ with $c=f(0)$. And also that $$\tag2\exp(x+y)=\exp(y)\exp(x)$$ for all $x,y$ because $x\mapsto \exp(x+y)$ is also a solution of $(1)$. Especially, $\exp(n)=\exp(1)\exp(1)\ldots\exp(1)=(\exp(1))^n$. In effect, because of $(2)$, the function $x\mapsto \exp(x)$ suspiciously behaves like exponentiation and is therefore usually suggestively written like exponentiation, i.e. we write $e^x$ instead of $\exp(x)$. Of course for this to make sense, we must define $e=\exp(1)$. It turns out that $\exp(1)\approx 2.71828$.

Hagen von Eitzen
  • 374,180