6

Just like $\pi$ is the ratio of a circle's circumference to its diameter? I know that the tangent line to the function $e^x$ has a slope of $e^x$ at that point, but is there some other geometric representation? Thanks!

Hanul Jeon
  • 27,376
Ovi
  • 23,737
  • I'd love to see an answer to this question that's expressed in terms of "standard" geometric objects like circles and rectangles, rather than functions like $1/x$. (I don't know of one myself.) – N. Virgo May 06 '13 at 02:48
  • @Nathaniel You may find the article in my answer interesting, though perhaps technically different from what you seek. – Gyu Eun Lee May 06 '13 at 03:22
  • @proximal thanks, that is indeed interesting! – N. Virgo May 06 '13 at 04:02

5 Answers5

8

Consider the area under the hyperbola $y=\frac{1}{x}$, above the $x$-axis, from $1$ to $a$. This area is $1$ precisely if $a=e$.

André Nicolas
  • 507,029
5

In this article http://arxiv.org/abs/0704.1282, Jonathan Sondow describes a geometric construction of the number $e$ that's different in flavor from the other answers. The idea is that his construction is a geometric representation of the identity $$\sum_{i=1}^\infty\frac{1}{n!}.$$

It's very readable for anyone who's familiar with convergence of sequences, so anyone who's taken and understood second-semester calculus.

Gyu Eun Lee
  • 18,793
  • Haha I'm actually in calc AB (equivalent of first semester) but I'll give it a shot! – Ovi May 06 '13 at 02:53
  • 1
    The article is actually pretty cool in several respects - not only does it geometrically prove that $e$ is irrational, it gives you a way to tell just how irrational it is. – Gyu Eun Lee May 06 '13 at 02:58
  • I don't have time to read it right now but it does look interesting and I'll look at it later – Ovi May 06 '13 at 03:01
3

As $\int_1^e \dfrac{1}{x} dx = 1$, we can say that $e$ is the length along the $x$-axis giving the area of $1$ beneath the curve $y= \dfrac{1}{x}$. (See picture.)

Kris Williams
  • 3,039
3

Normally we work with this as follows: we introduce the $\ln$ function as the function that measures the area bellow the hyperbola $xy=1$ from $x=1$ to some other point $x=t$ so that we can define it as:

$$\ln t=\int_1^t \frac{dx}{x}$$

Then you prove that this function possess the properties that you want. There's a number $x$ then such that you have $\ln x = 1$ and this number is what we call $e$ so that we have:

$$\ln e=\int_1^e \frac{dx}{x}=1$$

Now you have defined this number $e$ simply as the coordinate of the point $x$ such that the area bellow the hyperbola $xy=1$ from $x = 1$ to $x=e$ is unity. With some tricks them you can find estimates to this number and even show that it's transcedental.

For more information on the subject see Spivak's Calculus.

Gold
  • 26,547
1

I don't think it's just a matter of the tangent line at the general point having slope $e^x$. Rather, as the graph crosses the $y$-axis, the slope is exactly one. In fact, this gives us a way to approximate $e$ in the first place.

Examine the graphs of functions of the form $f(x)=a^x$. As $a$ increases, these get steeper. When $a=2$, the slope of the graph as it crosses the $y$-axis is around $0.69$. When $a=3$, the slope of the graph as it crosses the $y$-axis is about $1.09$. There is a very special number between $2$ and $3$ where the slope is exactly $1$. This number is probably a bit closer to $3$ than to $2$.

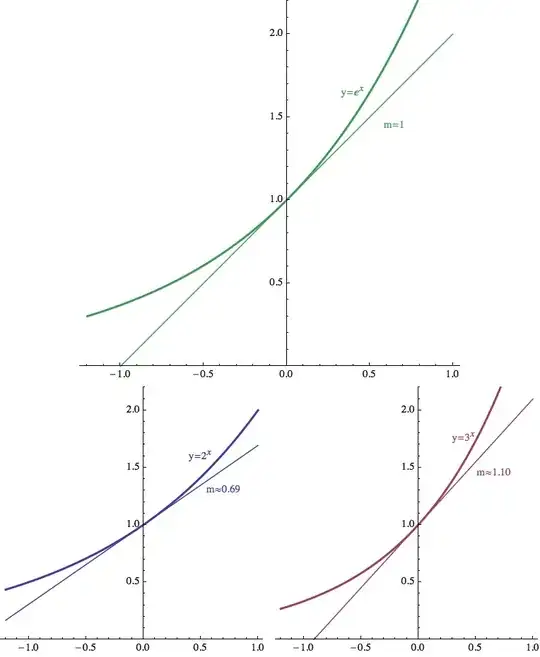
enter image description here

Mark McClure
  • 30,510