8

Let's take some popular numbers in math: $\pi$, $e$, $\sqrt{2}$ and $\phi$. The number $\pi$ is the ratio between the circumference and the diameter of a circle; $\sqrt{2}$ is the length of a diagonal of a unit square, $\phi$ is the length of a diagonal of a regular unit pentagon. It seems like $e$ is not a part of any reasonably familiar geometric shape.

Is this really so? By 'familiar geometric figure' I mean a geometric figure $F$ that hasn't been artificially constructed so that $e$ is somehow a part of it. By 'part' here I mean the ratio of something in $F$ and something else in $F$, the length of something in $F$, the area of $F$, maybe its perimeter, etc.

Antoni Parellada
  • 8,889
user132181
  • 2,726
  • 7
    One example could be that it's the $x$ such that $\int_1^x\frac{1}{t},\mathrm{d}t=1$. But I don't know if that's exactly what you're looking for. – Jam Aug 22 '14 at 10:28
  • Seems like an artificial geometric figure to me. It doesn't arise "naturally" in math if you forget its connection to $e$. – user132181 Aug 22 '14 at 10:31
  • 1
    I don't entirely understand what you mean by an "artificial geometric figure"; the area under the graph could be constructed outside of an $(x,y)$ plane just as a circle or square could be. – Jam Aug 22 '14 at 10:34
  • Well, guys... you know what I mean. I've tried as much as I could to convey my thoughts. – user132181 Aug 22 '14 at 10:37
  • Actually, your meaning still isn't entirely clear to me. Do you just want regular shapes? I don't see why the area under a graph is any more artificial than a circle. – Jam Aug 22 '14 at 10:39
  • I want the geometric figure to be "closer" to "classic geometry" rather than to calculus. Does that make any sense? – user132181 Aug 22 '14 at 10:40
  • 5
    Well I think therein lies your problem: $e$ wasn't known until calculus so it's unlikely to appear without it. – Jam Aug 22 '14 at 10:42
  • @EulCan I think you are completely right here. Turns out the question was dumb :( – user132181 Aug 22 '14 at 11:13
  • 4
    I wouldn't say that calculating the area of a piece of hyperbola is not sufficiently related to classic geometry. In this sense $\pi$ is related to the area of the possitive conic (circle and ellipse) and $e$ to the area of the negative one (hyperbola). – Josué Tonelli-Cueto Aug 22 '14 at 12:44
  • another thread Is there any geometric way to characterize e ? – Raymond Manzoni Feb 02 '21 at 10:05

2 Answers2

4

It may be a stretch, but a claim can be made that the catenary is a mesmerizing geometrical object that is all about the Euler constant.

Given by its expression:

$$f(x) = \cosh(x ) = \frac 1 2 \left(e^{x} + e^{-x}\right),$$

it is the average of exponential growth and decay:

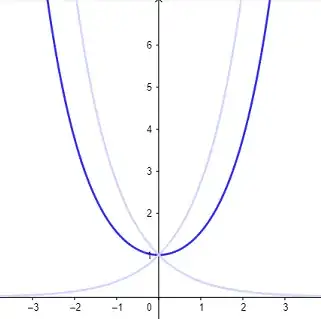
enter image description here

And although this implies that calculus is never left behind, it also results in a perfect architectural and engineering structure (with a minus in front): the catenary arc.

Casa Milà, Antoni Gaudí

Casa Milà, Antoni Gaudí

The equation of a catenary can be derived with a contrained (by the length of the chain) Euler-Lagrange equation assuming uniform physical properties.

It is not surprising that the catenary arc is described as "an arch of uniform density and thickness, supporting only its own weight, the catenary is the ideal curve," when it is (aside from constants) the only function to preserve the ratio between the arc length of any interval and the area subtended:

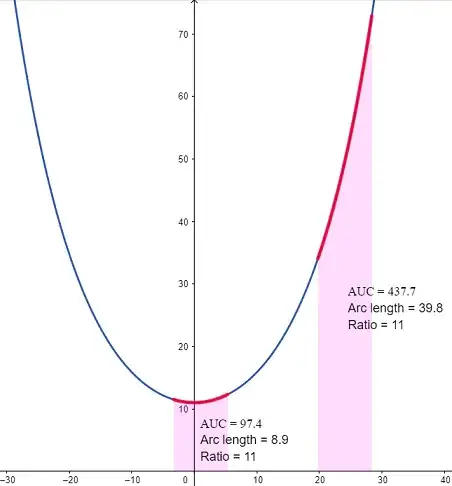
enter image description here

And although this may sound like it is steering off topic, it is a beautiful counterpoint to $e^x$ being its own integral (up to a constant). Further, this ratio between area under the curve and arc length corresponds to the scaling parameter $a$ in the general equation of the catenary $a \cosh(x/a),$ and can be interpreted as the interest rate in the continuous compounding formula $e^{x/a}.$ In a way a perfect arch is the physical picture of continuously compounded interest.

Antoni Parellada
  • 8,889
2

Consider the graph of the funcion $f(x) = a^x$, with $a > 0$. Well, $f(0) = 1$ in any way, but we want more. Looking at the tangent line to the graph at the point $(0,1)$, what is the base $a$ such that the inclination of the line is $1$? This happens just when $a = e = 2,718281828459045\ldots$. Analytically, this translates as $f'(x) = a^x \ln a $, and $f'(0) = 1$, since $\ln e = 1 $. Hope this helps.

Ivo Terek
  • 77,665