Method of characteristics for Burgers' equation with rectangular data

Question

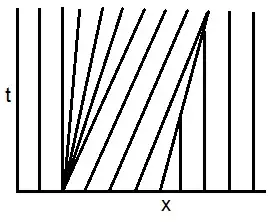
Using the method of characteristics, find a solution to Burgers' equation \begin{cases} u_t+\left(\frac{u^2}{2} \right)_x =0 & \text{in }\mathbb{R}\times(0,\infty) \\ \qquad \qquad \, \, u=g & \text{on } \mathbb{R} \times\{t=0\} \end{cases} with the initial conditions $$g(x)=\begin{cases} 0 & \text{if }x < 0 \\ 1 & \text{if }0 \le x \le 1 \\ 0 & \text{if }x > 1 \end{cases}$$

First, I realized that the equation $u_t+\left(\frac{u^2}{2} \right)_x =0$ is equivalent to this form: $$u_t+uu_x =0$$

Then should I generally follow the method of solution as outlined in the answer of this page?

Note that this is not a duplicate question of that page. Rather I want to know if that page can be used for my problem, even though my ICs are different.

By the way, the solution printed in my book (PDE Evans, 2nd edition, page 142) is

$$u(x,t) = \begin{cases} 0 & \text{if } x < 0 \\ \frac xt & \text{if } 0 < x < t \\ 1 & \text{if } t < x < 1 + \frac t2 \\ 0 & \text{if } x > 1 + \frac t2 \tag{$0 \le t \le 2$} \end{cases}$$

Answer 1

The variable $u$ is constant along the characteristic curves, which satisfy \begin{aligned} x'(t) & = u(x(t),t) \, , \\ & = u(x(0),0) \, . \end{aligned} Thus, the latter are straight lines in the $x$-$t$ plane, determined by the initial data. Here, the initial data is piecewise constant, i.e. we solve Riemann problems. As displayed in the figure below,

• characteristics separate in the vicinity of $x=0$, and a rarefaction wave occurs;
• characteristics cross in the vicinity of $x=1$, and a shock-wave occurs.

The rarefaction wave is a continuous self-similar solution, deduced from the self-similarity Ansatz $u (x,t)=v (\xi)$ with $\xi = x/t$. Indeed, $$ \partial_t u(x,t) + u(x,t)\, \partial_x u(x,t) = \left(v(\xi) - \xi\right) \frac{v'(\xi)}{t} \, , $$ and thus, $v(\xi) = \xi$ or $u(x,t) = x/t$. The shock speed $s$ is given by the Rankine-Hugoniot jump condition: $$ s = (1+0)/2\, . $$ As long as the rarefaction and the shock don't interact, the solution is therefore $$ u(x,t) = \left\lbrace \begin{aligned} & 0 &&\text{if }\; x\leq 0 \, , \\ & x/t &&\text{if }\; 0\leq x\leq t \, , \\ & 1 &&\text{if }\; t \leq x < 1+ t/2 \, ,\\ & 0 &&\text{if }\; 1+t/2 < x \, , \end{aligned} \right. $$ valid for times $t<t^*$ such that $t^* = 1 + t^*/2 = 2$. At the time $t^*$, both waves interact. The new shock speed is determined from the Rankine-Hugoniot condition $$ x'(t) = (x(t)/t+0)/2 \, , $$ with initial shock speed $x'(t^*) = s$. Hence, the solution for $t\geq t^*$ is $$ u(x,t) = \left\lbrace \begin{aligned} & 0 &&\text{if }\; x\leq 0 \, , \\ & x/t &&\text{if }\; 0\leq x< \sqrt{2t} \, , \\ & 0 &&\text{if }\; \sqrt{2t} < x \, . \end{aligned}\right. $$

Answer 2

Follow the method in http://en.wikipedia.org/wiki/Method_of_characteristics#Example:

$\dfrac{dt}{ds}=1$ , letting $t(0)=0$ , we have $t=s$

$\dfrac{du}{ds}=0$ , letting $u(0)=u_0$ , we have $u=u_0$

$\dfrac{dx}{ds}=u=u_0$ , letting $x(0)=f(u_0)$ , we have $x=u_0s+f(u_0)=ut+f(u)$ , i.e. $u=F(x-ut)$

$u(x,0)=\begin{cases}0&\text{if}~x<0\\1&\text{if}~0\le x\le1\\0&\text{if}~x>1\end{cases}$ :

$\therefore u=\begin{cases}0&\text{if}~x-ut<0\\1&\text{if}~0\le x-ut\le1\\0&\text{if}~x-ut>1\end{cases}=\begin{cases}0&\text{if}~x<0\\1&\text{if}~0\le x-t\le1\\0&\text{if}~x>1\end{cases}$

Hence $u(x,t)=\begin{cases}0&\text{if}~x<0\\1&\text{if}~0\le x-t\le1\\0&\text{if}~x>1\\c&\text{otherwise}\end{cases}$