Finding weak solutions of conservation law $u_t + (u^4)_x = 0$

Question

Consider the conservation law $$ u_t + (u^4)_x = 0, $$ (a) Find the solution at $t=1$ with the following initial condition: $$ u(x,0) = \left\lbrace\begin{aligned} &1 && x<0 \\ &2 && 0\leq x \leq 2 \\ &0 && x>2 \end{aligned} \right. . $$ (b) Solve the Riemann problem (You must consider both $u_l>u_r$ and $u_l<u_r$): $$ u(x,0) = \left\lbrace\begin{aligned} &u_l && x<0 \\ &u_r && x>0 \end{aligned} \right. . $$ (c) Find the Riemann solution at $x/t = 0$.

Try:

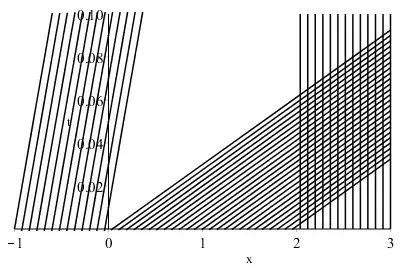
The characteristic are given by $x = 4 g(r)^3 t + r $ where $r$ is parameter. so we have

$$ x = \begin{cases} 4t+r, & r<0 \\ 8t+r, & 0 \leq r \leq 2 \\ r, & r > 2 \end{cases} $$

We have two shocks formations at $x=0$ and $x=2$ for $t=0$. We first consider the shock at $x=0$, using R=H condition, we want

$$ \xi_1'(t) = \frac{ 2^4 - 1^4 }{2-1} = 15 \implies \xi_1(t) = 15t $$

and at $(x,t) = (2,0)$ we have

$$ \xi_2'(t) = \frac{ - 2^4 }{0-2} = 8 \implies \xi_2(t) = 8t+2$$

So we can write our solution for part a

$$ \boxed{ u(x,t) = \begin{cases} 1, & x < 15 t \\ 2, & 15t < x < 8t+2 \\ 0, & x > 8t+2 \end{cases} } $$

IS this correct? I have a question as to what is it that they are asking in c)?

Answer 1

(a) Here is a plot of the characteristic lines in the $x$-$t$ plane.

Since the flux $u \mapsto u^4$ is convex, the classical theory for entropy solutions of conservation laws applies. Without entering into details, the rarefaction wave generated at $x=0$ and the shock wave generated at $x=2$ leads to the solution $$ u(x,t) = \left\lbrace \begin{aligned} & 1 && x \leq 4 t \\ & \sqrt[3]{x/(4t)} && 4 t \leq x \leq 32 t\\ & 2 && 32 t \leq x \leq 2 + 8 t \\ & 0 && x \geq 2 + 8 t \end{aligned} \right. $$ valid for small times $t < 1/12$. For larger times, one must compute the interaction of the rarefaction with the shock (see related posts on this site, e.g. this one). Here, a shock wave is obtained, whose position is governed by the Rankine-Hugoniot condition $$ \frac{\text d x_s}{\text d t} = \frac{[u^4]}{[u]} = \frac{(\frac14 x/t)^{4/3} - 0^4}{(\frac14 x/t)^{1/3} - 0} $$ with initial position $x_s(1/12) = 8/3$, leading to the shock trajectory $x_s(t) = 8 \sqrt[4]{4t/27}$. At $t=1$, we have $x_s(1)\approx 4.9632$ and $$ u(x,t) = \left\lbrace \begin{aligned} & 1, && x \leq 4 , \\ & \sqrt[3]{x/4}, && 4 \leq x < x_s(1) , \\ & 0, && x > x_s(1) . \end{aligned} \right. $$

(b) If $u_l > u_r$, the Riemann solution is a shock wave with Rankine-Hugoniot speed $s = \frac{(u_r)^4 - (u_l)^4}{u_r - u_l}$: $$ u(x,t) = \left\lbrace \begin{aligned} & u_l, && x < s t , \\ & u_r, && x > s t . \end{aligned} \right. $$ Otherwise, if $u_l < u_r$, it is a rarefaction wave $$ u(x,t) = \left\lbrace \begin{aligned} & u_l, && x \leq 4 (u_l)^3 t , \\ & \sqrt[3]{x/(4t)}, && 4 (u_l)^3 t\leq x \leq 4 (u_r)^3 t, \\ & u_r, && x \geq 4 (u_r)^3 t . \end{aligned} \right. $$

(c) Asking to find the Riemann solution at $x/t = 0$ is rather straightforward: it is the same as asking to find the solution at $x = 0$ for nonzero time.