This is an old PDE qual problem and I seem to be lacking proper background to solve.
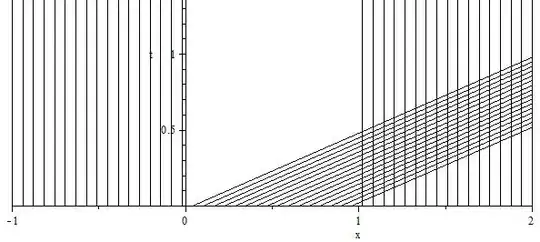
Solve $u_t+uu_x = 0$, where the initial data is given by $$f(x) = \begin{cases}2, &0<x<1\\ 0, & \text{otherwise} \end{cases}.$$ Moreover, show that the solution has both rarefaction and shock wave, and decide whether the rarefaction wave catches the shock. Characterize the location and velocity of the waves.
What I am able to do is to use the method of characteristics to start as: $$u(t,x) = \begin{cases}2,&ut<x<ut+1\\0,&x\leq ut \,\,\,\vee \,\,x\geq ut+1 \end{cases}.$$
After this, how does one find the shock and rarefaction waves? I am following Introduction to Partial Differential equations by Peter Olver and the text says rarefaction and shock occurs when $f'(x)>0$ and $f'(x)<0$, respectively. But this does not help at all in this problem.