Consider the following: $$u_t+uu_x=0, ~~ t>0$$
and the initial data: $$ u(x,0)=\begin{cases} 1,&\text{ if }x\in[0,1]\text{ and } \\ 0,&\text{ otherwise. } \end{cases}$$
I have found a solution to the above problem like the following picture but is valid only for $t<2$ ...I do not know how to extend this solution for all $t>0$. Any hint please?
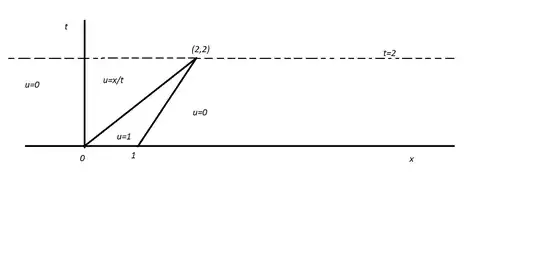
Remark: I have found this weak solution drawing the characteristic lines of the problem and applying a shock and fan wave where the characteristics intersect and where a "gap" is created, respectively. I confirmed this solution using Runkine - Hugionot theorem.