2

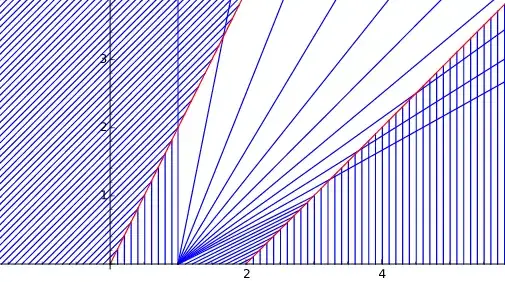
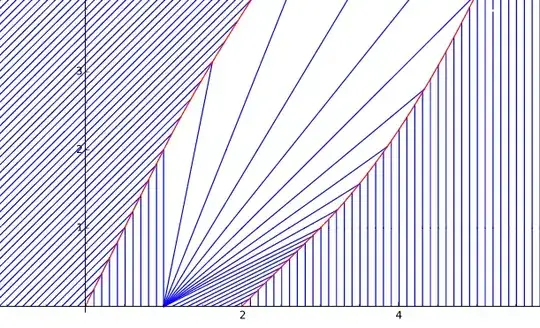
I'm confident I've solved all but the last segment of this problem, to which I have an answer that just doesn't seem right. The problem is to solve the inviscid Burgers' equation $$u_{t}+uu_{x}=0$$ for $u(x,t)$ with the initial condition that for $t=0$, $u(x,0)$ is respectively 1, 0, 2, and 0 for $x<0$, $0<x<1$, $1<x<2$ and $x>2$.

We have the usual shocks parametrized as $x(t)=t/2$ and $x(t)=t+2$, as well as a rarefaction wave in $0<x<2t$. My issue is in calculating the new shock path for $t>1$ when the shock encounters the rarefaction wave. From the jump condition with $u_l=1$, $u_r=x/t$ the shock solves the differential equation $\dot{x}=\frac{1+x/t}{2}$ with the initial condition $x(1)=1$, but upon solving this I find $x(t)=t$, which contradicts my intuition - it doesn't seem reasonable that the shock would suddenly become parallel to the characteristics to its left. Can anyone tell me whether my answer or intuition is correct? I'm hoping at least one of them is...

BGreen
  • 850
  • 1
    Since rarefaction emanates from $x=1$, the velocity within it is $u=(x-1)/t$, rather than $x/t$. This throws off the rest of your calculation. –  Nov 23 '15 at 04:11

1 Answers1

8

After the basic shock waves $x=t/2$ and $x=t+2 $ (shown in red) are accounted for, the characteristics look like this.

basic

This picture is correct for times $t<1$, but needs two adjustments after that. Note that the solution within rarefaction wave is $u(x,t) = (x-1)/t$.

Rarefaction catches up with shock on the right: $x=3$, $t=1$.

From this point on, the position of this shock satisfies $$ \frac{dx}{dt} = \frac12 \left( \frac{x-1}{t} + 0 \right) = \frac{x-1}{2t} $$ hence $x(t) = 2\sqrt{t} +1$.

Shock on the left catches up with rarefaction: $x=1$, $t=2$.

From this point on, the position of this shock satisfies $$ \frac{dx}{dt} = \frac12 \left( 1 + \frac{x-1}{t} \right) = \frac{x-1+t}{2t} $$ hence $x(t) = t-\sqrt{2t}+1$.

Notice that in both cases the space-time trajectory of the shock becomes parabolic: this always happens when a rarefaction wave interacts with a constant velocity field.

Plotting the new trajectories of shocks, and terminating the characteristics accordingly, we get the following picture (one has to look closely to notice the curvature of red curves).

final

Final battle: two shocks come together

At the time $t=6+4\sqrt{2} \approx 11.5$ (off the chart above), the two shock waves meet at $x=5+2\sqrt{2}$. At this moment, rarefaction ceases to exist. The single shock wave forms, separating the velocities $1$ and $0$. It propagates according to the equation $$ x(t) = 5+2\sqrt{2} + \frac12 (t-6-4\sqrt{2}),\quad t\ge 6+4\sqrt{2} $$