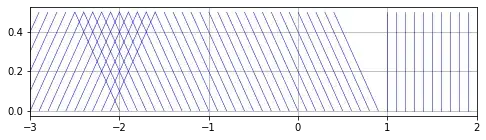
Find the generalized entropic solution of the Cauchy problem $$u_t+\left ( \frac{u^2}{2} \right )_x=0,u|_{t=0}=u_0$$ When $x<-2\Rightarrow u_0(x)=1$, when $-2<x<1\Rightarrow u_0(x)=-1$, when $x>1\Rightarrow u_0(x)=0$
I know it is a nonlinear Burgers equation $$u_t+\left ( \frac{u^2}{2} \right )_x=0, \; u(x, 0) = \begin{cases} 1, & \text{if} x < -2, \\ -1, & \text{if } -2 < x < 1, \\ 0, & \text{if } x > 1. \end{cases}$$
But there's a big problem with jumps. My attempt:
I will write the Burgers equation as a system of ordinary differential equations
$$ \frac{dx}{dt} = u, \quad \frac{du}{dt} = 0 $$
The characteristic equations become - $x(t) = ut + x_0$
- At $x<-2$, $u=1$, so $x(t)=t+x_0$. Hence, $x_0=x-t$ and the solution $u=1$ for $x<t-2$.
- At $-2<x<1$, $u=-1$, so $x(t)=-t+x_0$. Hence, $x_0=x+t$ and the solution $u=-1$ for $x>-t-1$ and $x<-t+1$.
- At $x>1$, $u=0$, so $x(t)=x_0$. Hence, $x_0=x$ and the solution $u=0$ for $x>1$.
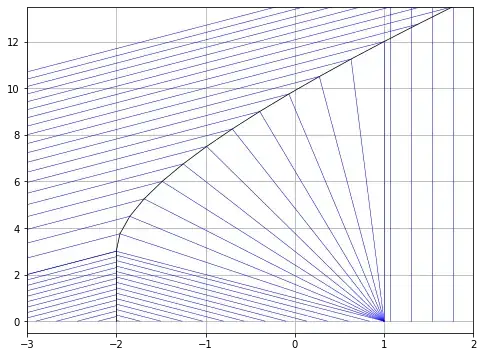
We have regions where jumps in the value of $u$ are possible. Consequently, we must treat them according to the entropy condition, which states that jumps must propagate at a rate that is the average of the velocities on the two sides of the jump. In our case, at the point $x=-2$ the jump goes from $1$ to $-1$, so that the speed of the jump is $(1 - 1) / 2 = 0$, which means that the jump is not moving. Similarly, at $x=1$ the jump goes from $-1$ to $0$, so the speed of the jump is $(-1 + 0) / 2 = -1.2$. And I got this solution
$$ u(x, t) = \begin{cases} 1, & \text{if } x < t - 2, \\ -1, & \text{if } -t - 1 < x < \min(-t + 1, 1 - 0.5t), \\ 0, & \text{if } x > \max(1 - 0.5t, -t + 1) \end{cases} $$
Did I get the cases and the jumps right? If there is an easier way, could you show me a simpler solution?