Cartesian Product of Two Countable Sets is Countable

Question

How can I prove that the Cartesian product of two countable sets is also countable?

Answer 1

In your answer you use Cantor's pairing function. It is an important function indeed. However using Cantor-Bernstein's theorem we only need to find an injection from $\mathbb N\times\mathbb N$ into $\mathbb N$.

A useful example is: $$f(m,n) = 2^m\cdot 3^n$$

If $f(m,n)=f(l,k)$ then by the fundamental theorem of arithmetics we have that $m=l, n=k$.

We now can find an injection $g\colon\mathbb N\to\mathbb N\times\mathbb N$, for example $g(n)=(0,n)$.

Now Cantor-Bernstein's theorem tells us that if $f\colon A\to B$ and $g\colon B\to A$ are two injective functions, then there is a bijection from $A$ into $B$.

From this to $\mathbb N^k$ being countable, you can either go with induction, as you suggested, or map $(m_1,\ldots,m_k)$ to $p_1^{m_1}\cdot\ldots p_k^{m_k}$, where $p_i$ is the $i$-th prime number.

Answer 2

So I know $\mathbb{N} \times \mathbb{N} \to \mathbb{N}$ via (provided from class proof): $$f(x,y) = \frac{(x + y - 2)(x + y - 1)}{2}$$ Then it would mean that two countable sets, $A$ and $B$, can be set up as $f:\mathbb{N} \to A $ and $g: \mathbb{N} \to B$. This points to: $$f \times g : \mathbb{N} \times \mathbb{N} \to A \times B$$ There is now a surjection $\mathbb{N} \times \mathbb{N}$ to $A \times B$ $\implies$ $A \times B$ is also countable. So then induction can be used in the number of sets in the collection.

Answer 3

We have a general result.

We use the notation $[n] = \{0,1,2,3,\cdots ,n-1 \}$.

Proposition 1: Let $A$ be a set and let ${(G_k)}_{k \in \mathbb N}$ be a countable family of sets satisfying:

$\tag 1 \text{Each } G_k \text{ is a nonempty finite subset of } A \text{ with cardinality } \alpha_k$
$\tag 2 \text{The family } G_k \text{ of sets is a partition of } A$

For each $k \ge 0$ let there be given a bijective mapping

$\tag 3 \tau_k: [\alpha_k] \to G_k$

Then there exist a bijection $f: \mathbb N \to A$.
Proof
For each $m \in \mathbb N$ let $K_m = \sum_{i=0}^{m-1} \alpha_i$; note that $K_0 = 0$.
For each $n \ge 0$, define $\lambda(n) = \text{max(} \{ m \, | \, K_m \le n \} \text{)}$.
Since $0 \le n - K_{\lambda(n)} \le \alpha_{\lambda(n)} - 1$, we can define a function

$\quad f(n) = \tau_{\lambda(n)}(n - K_{\lambda(n)})$

It can be shown that this function $f$ is a bijective correspondence between $\mathbb N$ and $A$. $\quad \blacksquare$

Note that we defined an explicit function based on a sequence of given functions, so we are not using any form of the Axiom of Choice. This is a subtle point - we know the functions exist but an axiom in necessary if we want to pull them together out of 'thin air'.

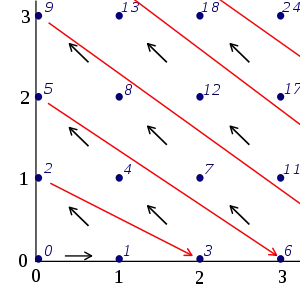
Exercise: Define a bijective correspondence between $\mathbb N$ and $\mathbb N \times \mathbb N$ using the Cantor pairing function, as described in Wikipedia as

---

Although using the summation notation might be using some implied induction/recursion, Proposition 1 describes a function directly. So the function doesn't have to carry an 'internal state baggage' as it executes. In practice, the mechanism will be much easier to program/calculate than it might appear.

Following is a Python program that implements the bijection.

L = 1
while True:
    for y in range(0, L):
        x = L - 1 - y
        print((x,y), '', end='')
        if x==0:
            break
    if L == 10:
        print('...', end='')
        print("\nProgram stopping after printing", L, 'levels.')
        break
    else:
        L = L + 1
        continue 

OUTPUT:

(0, 0) (1, 0) (0, 1) (2, 0) (1, 1) (0, 2) (3, 0) (2, 1) (1, 2) (0, 3) (4, 0) (3, 1) (2, 2) (1, 3) (0, 4) (5, 0) (4, 1) (3, 2) (2, 3) (1, 4) (0, 5) (6, 0) (5, 1) (4, 2) (3, 3) (2, 4) (1, 5) (0, 6) (7, 0) (6, 1) (5, 2) (4, 3) (3, 4) (2, 5) (1, 6) (0, 7) (8, 0) (7, 1) (6, 2) (5, 3) (4, 4) (3, 5) (2, 6) (1, 7) (0, 8) (9, 0) (8, 1) (7, 2) (6, 3) (5, 4) (4, 5) (3, 6) (2, 7) (1, 8) (0, 9) ...
Program stopping after printing 10 levels.