2

I know $ \omega ^ 2 $ is countable, but I'm unable to find a bijection from $ \omega * \omega \rightarrow \omega $

This should be simple, but I'm very stuck.

M.Sina
  • 1,690
Simply Brian
  • 261
  • 3
    Hint: lay out $\omega^2$ in a quarter-infinite grid, as the set of points $\langle x,y\rangle$ with $x,y\in\mathbb{N}$. Can you see how to enumerate all the points in this grid? – Steven Stadnicki Mar 01 '13 at 07:01

2 Answers2

1

This picture shows one way:

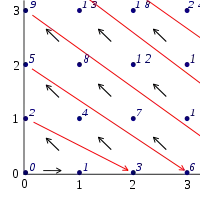
enter image description here

If you have to describe this bijection $\varphi:\omega\times\omega\to\omega$ more formally, it’s worth spending some time trying to work out a formula for $\varphi(a,b)$ in terms of $a$ and $b$; all you need is a little ingenuity and the familiar formula for the sum of the first $n$ positive integers, $\sum_{k=1}^nk=\frac12n(n+1)$. If you get stuck, you’ll find much help in this Wikipedia article.

Brian M. Scott
  • 616,228
1

think about what it actually is on the inside:

$$\begin{array}? \omega^2 = &\{& 0,1,2,3,\ldots, \\ && \omega,\omega+1,\omega+2,\omega+3,\ldots, \\ && 2\omega,2\omega+1,2\omega+2,2\omega+3,\ldots,\\ && 3\omega,3\omega+1,3\omega+2,3\omega+3,\ldots, \\ && \vdots \\ &\}& \end{array}$$

now can easily see why it is in bijection with $\mathbb N^2$ and hence $\mathbb N$ hence countable.