Bijection for a function $ \mathbb{Z}^+ \times \mathbb{Z}^+$ to $\mathbb{Z}^+ $

Question

Possible Duplicate:
Countable Sets and the Cartesian Product of them

Consider the following question:

Describe a function $ \mathbb{Z}^+ \times \mathbb{Z}^+$ to $\mathbb{Z}^+ $ that is one-to-one and onto (bijection).

This is quite a mind twister. Namely, anything of like $f(x,y) = x + y$, $f(x,y) = xy$, etc. is neither one-to-one or onto.

I'm quite lost on this one. Thoughts?

Maybe the following equivalent problem is more intuitive: consider the lattice of all points in the first quadrant with integer coordinates. Can you draw a curve which passes through every lattice point? — user7530, Oct 14 '11 at 01:14

score 3 · Answer 1 · answered Oct 14 '11 at 01:14

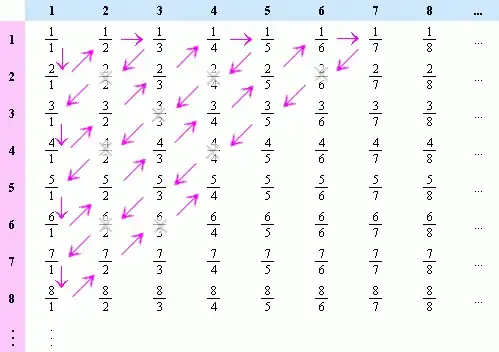
There are lots of ways to go at this question. The general idea is to not try to explicitly write a function (at first), but to instead realize that this just asks you to count all the pairs of natural numbers. Literally, count them, one at a time, leaving no number out and skipping no counting number.

For example, one might associate $(1,1)$ with $1$, $(1,2) \to 2$, $(2,1) \to 3$, $(1,3) \to 4$, etc. (Draw a picture to see what I'm doing).

To turn that into an explicit function isn't so bad once you see the pattern.

Or you might spiral, or anything. Alternatively, if you just have to show that one exists, you could map $(n_1, n_2) \to 2^{n_1}\cdot 3^{n_2}$ (why is this injective?) and $n \to (1, n)$ (obviously injective. Then we have injections from one into the other, and so we have that they have the same cardinality.

Is that a good start?

score 3 · Accepted Answer · edited Oct 14 '11 at 01:17

3

picture $\mathbb{Z}^+$ x $\mathbb{Z}^+$ as an infinite square of dots. It should have 2 sides.

now start counting as follows: Start with the first dot. Then follow the dot to the right of it. Then the dot above the first one. Then the dot above this last dot. Now count diagonally to your down-right. Once you've reached the side of the infinite square, proceed to the dot to the right of the one you stopped. then diagonally up-left-ward until you reach the left side of the square. then go up and diagonally towards down-right. proceed...

It should look like this:

enumerating Z^+ x Z^+

(from homeschoolmath.net)

if you rotate this infinite square by $\frac{\pi}{2}$

edited Oct 14 '11 at 01:17

t.b.

78,116

answered Oct 14 '11 at 01:15

Henrique Tyrrell

1,709

I like how rational your integers are. – davidlowryduda Oct 14 '11 at 01:19
This is definitely the way I think about. Draw it graphically, imagine trying to lay a number line on top of a grid by spiraling or zig-zagging, then figure out what the actual function or pattern is by writing down the first bunch of relations. – Jonathan Beardsley Oct 14 '11 at 01:27
Took me a while to wrap my head around this, but I get it now. Thanks. – David Chouinard Oct 14 '11 at 02:35

score 2 · Answer 3 · answered Oct 14 '11 at 01:21

Assuming ${\mathbb{Z}}^{+}$ are positive integers:

$f(x,y)=2^{x-1} (2y-1)$

For nonnegatives:

$f(x,y)=2^x (2y+1) - 1$

Every natural number can be uniquely decomposed as a power by two times an odd number. This is a bijection.

For another example: pairing function.

Bijection for a function $ \mathbb{Z}^+ \times \mathbb{Z}^+$ to $\mathbb{Z}^+ $

3 Answers3