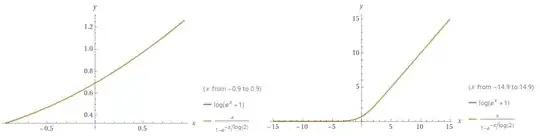
Trying to split the logarithm of the sum of two exponential functions (this question), I found the following approximation for the Softplus function $f(x)=\ln(1+e^x)$:
$$\ln(1+e^x) \approx \begin{cases} \frac{x}{1-e^{-\frac{x}{\ln(2)}}},\quad x\neq 0\\ \ln(2),\quad x=0\end{cases}$$
From now on I will omit the domain issue at $x=0$ for simplicity, but keep it in mind for the following approximations based in this formula.
And I want to know if it is a known approximation and how useful it is. I just added to the Wikipedia for the Softplus function, and I am surprised it wasn't mentioned before. The maximum error is below $0.0092$, and the plot is quite close:
The error figure could be improved using $f(x,a)=\frac{x}{1-e^{-\frac{x}{a}}}$ with $\frac{1}{a}\approx 1.428666$ but it change the value at $x=0$, which for my application was important to keep it as $f(0)=\ln(2)$ (since matches with $\ln(e^0+e^0)$).
With this approximation I could split LogSumExp(x,y): $$\ln(e^x+e^y) \approx \frac{xe^{\frac{x}{\ln(2)}}-ye^{\frac{y}{\ln(2)}}}{e^{\frac{x}{\ln(2)}}-e^{\frac{y}{\ln(2)}}}$$
or simply $x+\ln(2)$ when $x\equiv y$, and it works quite good if $e^x+e^y$ is not too close to zero.
But unfortunately it was still too complicated for what I was aiming for. Finally I used the Taylor's expansion of $\ln(1+e^x)\approx \ln(2)+\frac{x}{2}+\frac{x^2}{8}+O(x^4)$ from were I got $\ln(e^x+e^y)\approx \ln(2)+\frac{x+y}{2}+\frac{(y-x)^2}{8}$.
Also leads to the approximation for positive $x,y$: $$\ln(x+y)\approx \frac{x^{\frac{1}{\ln(2)}}\ln(x)-y^{\frac{1}{\ln(2)}}\ln(y)}{x^{\frac{1}{\ln(2)}}-y^{\frac{1}{\ln(2)}}}$$
Please remember is undefined at $x=y$, but it just required to be defined piecewise as $\ln(2x)$ or $\ln(2y)$ where they match.
I don't know if these approximation are wide known or useful, for example for finding the distribution of the sum of Log-Normal random variables (any reference will be appreciated).
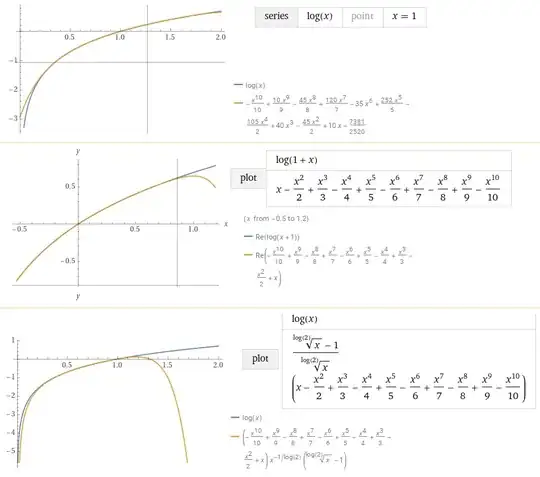
I played a bit with them and as example I could found the following approximations: $$\frac{\ln(1+y^{\ln(2)})}{\ln(y^{\ln(2)})}\approx \frac{y}{y-1}$$ when kind of matches for $y>0$ plot here.
or more interesting: $$\ln(x+1)\approx \frac{x^{\frac{1}{\ln(2)}}}{\left(x^{\frac{1}{\ln(2)}}-1\right)}\ln(x)$$
I don't know if some recurrence relation could be developed through it, but I tried to use it for the Taylor's expansion of $\ln(x)$ at $x=0$ (which is undefined), and it looks like $\frac{\left(x^{\frac{1}{\ln(2)}}-1\right)}{x^{\frac{1}{\ln(2)}}}\text{Taylor}[\ln(x+1)]$ behaves better than the Taylor's expansion of $\ln(x)$ at $x=1$ near $x=0$ (see the plot here).
Added later: Using these formulas I found here that some pretty descent approximations could be done for the logarithm function - check its plot here: $$\ln(x)\approx \dfrac{(x-1)\left(x+x^{\ln(2)}\right)}{x\left(1+x^{\ln(2)}\right)}$$
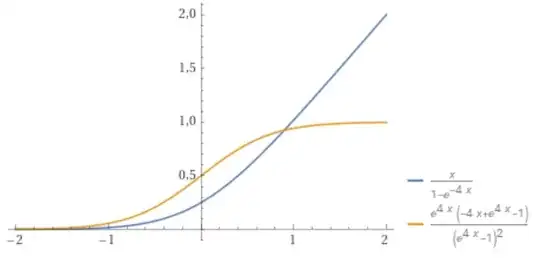
Another interesting fact of the approximation is that the following function for a real-valued parameter $a>0$: $$g(a,x) = \begin{cases}\frac{1}{a},\quad x=0 \\ \displaystyle{\frac{x}{1-e^{-ax}}},\quad x\neq 0 \end{cases}$$ could be a smooth approximation for the ramp function $\frac{x+|x|}{2}$ that can be arbitrarily close as $a\to\infty$ (the maximum absolute error is $1/a$), as you could check in Desmos.
Also, the derivative: $$g'(a,x)=\begin{cases} \frac12,\quad x=0\\ \frac{\partial}{\partial x} g(a,x),\quad x\neq 0\end{cases}$$ makes a nice smooth approximation of the unitary step function, and also tells you that the slope of $g(a,x)$ at $x=0$ is always $\frac12$ for finite $0<a<\infty$.
But I don't know why they are not listed as examples for the Wikipedia pages of Rectifier functions neither as Sigmoid functions, and I don't know if it has been used already as a ReLU function.