1

I need to construct a function $f\in C^\infty(\mathbb{R})$, such that $$f(x)=\left\{\begin{aligned} &0,\quad x\leqslant 0,\\ &x,\quad x\geqslant 1. \end{aligned}\right.$$ I already know that we can construct some smooth functions using something like $e^{-\frac{1}{x}}$, but I don't know how to do this one, can anyone give me some help?

Exjudger
  • 31
  • 2
    Try constructing a function $g \in C^{\infty}\left(\mathbb{R}\right)$ such that $$g(x)=\left{\begin{aligned} &0,\quad x\leqslant 0,\ &1,\quad x\geqslant 1. \end{aligned}\right.$$ Then $xg(x)$ gives you your desired function. – Shiva May 21 '23 at 11:40
  • Exactly. The so-called cutoff function, right? – Exjudger May 21 '23 at 11:44
  • 3
    A smooth bump function with support $(0,1)$ will have as its integral a smooth step function. Alternatively, consider MSE Question 846743. – Jam May 21 '23 at 13:48
  • @Shiva I tried your idea and it works, but the transition has a waving-like behavior. I tried by integrating a smooth cut-off function and it works without the waving (first and second derivatives kept their signs unchanged during the transitions). I added as an answer. – Joako Jul 17 '23 at 22:10
  • in this other question someone named @RaymondManzoni show an approximation that could be useful if you drop accuracy: $$f(x)=\dfrac{x}{1-e^{-8x}}$$ Its a sigmoid curve integrated, so is not exactly zero for negative values naither $x$ for possitive ones, but fit them quite accurately. – Joako Jul 19 '23 at 16:57
  • you could try some by integrating some cummulative distribution functions. – Joako Feb 24 '24 at 13:29

2 Answers2

1

I don't fully got your question, but I believe you are looking something like this function: $$h(x)=\begin{cases} 0,\quad x\leq -\frac18 \\ x,\quad x\geq \frac18\\ \int\limits_{-\frac18}^x \frac{1}{1+\exp\left(\frac{32u}{64u^2-1}\right)}\ du,\ \text{otherwise} \end{cases}$$

which makes a smooth transition from $f(x)=0$ into $f(x)=x$.

I built it following the method shown in Wikipedia for smooth Bump functions.

You could see the function on Desmos: Desmos example

Added later

In this answer it is found a series expansion for a similar function.

Joako
  • 1,380
0

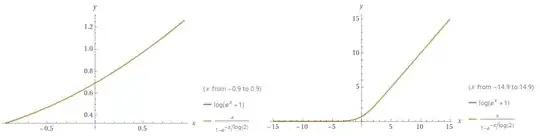
Asking a different question I found that there is a simple smooth version of the ramp function named in Wikipedia as Softplus function:

$$f(x) = \ln(1+e^x)$$

Achieves what you are aiming to do (you just need to displace and scale it - as example $f(8x-4)$), and it is smooth since its derivative is the Logistic function.

plot

Also, this function could be approximated by: $$\ln(1+e^x) \approx \begin{cases} \frac{x}{1-e^{-\frac{x}{\ln(2)}}},\quad x\neq 0\\ \ln(2),\quad x=0\end{cases}$$

as could be seen in their plot:

comparison of the plots

You could find other approximations in this Wikipedia page: Rectifier functions.

Joako
  • 1,380