0

After giving this answer to a question trying to find a smooth transition between $f(x\leq 0)=0$ and $f(x\geq 1)=x$ through the integral of a smooth transition function:

$$h(x)=\begin{cases} 0,\quad x\leq -1, \\ x,\quad x\geq 1, \\ \int\limits_{-1}^x \frac{1}{1+\exp\left(\frac{4u}{u^2-1}\right)}\ du,\ \text{otherwise} \end{cases}$$

which derivative makes a smooth transition from $f(x\leq 0)=0$ into $f(x\geq 1)=1$.

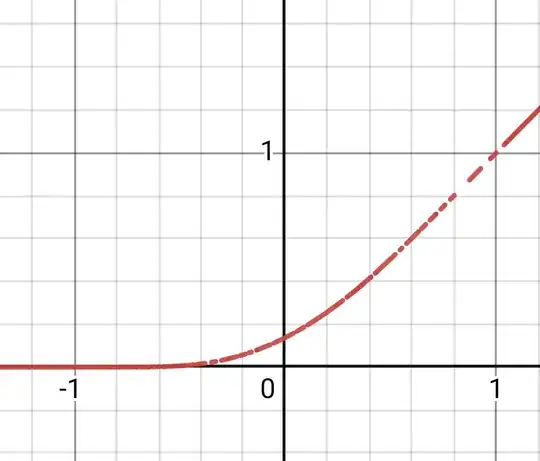
You could see this function on Desmos: function on Desmos

Even when the plot looks like a quite "innocent" function, given I have been unable to find a closed-form to the integral (if you now it please share it in the answer), I then tried to find a good polynomial approximation to $h(x)$ on the interval $x\in (-1,\ 1)$, but Wolfram-Alpha don't show any series expansion for this function (power series like Taylor's, Laurent's, Puiseux's, Padé approximants, etc).

By playing on Desmos the best simple fit I found on $x\in (-1,\ 1)$ is the function $\hat{h}(x) =\left|\frac{x+1}{2}\right|^{2.5}$ but is not really good neither: it is not smooth, as a polynomyal expansion should be.

best fit so far

so my question is:

It is possible to find a power series approximation to the function $h(x)=\int\limits_{-1}^x \frac{1}{1+\exp\left(\frac{4u}{u^2-1}\right)}\ du$ on $x\in(-1,\ 1)$? (centered at $x=0$ if possible)

Joako
  • 1,380
  • 1
    Possible frame change. What makes a "good" approximation depends on what you want the approximation for. In your example a (cubic) spline with nodes as $(-1,0)$ and $(1,1)$ with derivatives $0$ and $1$ respectively might serve even though it is not infinitely differentiable. – Ethan Bolker Jul 19 '23 at 15:47
  • @EthanBolker you are right, "good" is ambiguous (which is in parenthesis). I was just uploading a comment about the example I give is not smooth as a power series approximation should be. The spline example is a fit for the original answer also, I am looking for a fit for the curve given by the integral $h(x)$. – Joako Jul 19 '23 at 15:50
  • @EthanBolker I change anyway the question to focus it on $h(x)$. Thanks for commenting. – Joako Jul 19 '23 at 15:53
  • Since you have the integral you like as smooth approximation, why not take its Taylor expansion at x=-1? – trula Jul 19 '23 at 15:53
  • @trula I tried to find it unsuccesfully, since bump functions has points were analyticity is lost I got into problems. Maybe you could do it better. – Joako Jul 19 '23 at 15:56
  • 1
    An approximate solution : $\dfrac x{1-\exp(-7.7 x)}$ – Raymond Manzoni Jul 19 '23 at 16:00
  • @RaymondManzoni that function fits quite good, How you found it?.. I failed to do a Taylor expansion at $x=-1$, now working at $x=0$ and so far it behave worst than yours $$\hat{h}(x)=0.13775+\frac{x}{2}+\frac{x^2}{2}-\frac{x^4}{12}-\frac{13x^6}{90}$$ – Joako Jul 19 '23 at 16:20
  • 1
    Well the derivative is very similar to a sigmoid function that allow some mixing. Anyway you want $x$ for $x$ large combined with $0$ for negative values. $\dfrac x{1-\exp(-7.5 x)}$ appears a little better... – Raymond Manzoni Jul 19 '23 at 16:27
  • @RaymondManzoni Its much more better! really nice function: you should give something like $$f(x)=\dfrac{x}{1-e^{-8x}}$$ as answer to the mentioned question – Joako Jul 19 '23 at 16:30
  • @RaymondManzoni I just found the mentioned smooth transition is not exactly zero for negative values of $x$. Its still a nice function, but it don't fully fulfill what is asked on the other question. – Joako Jul 19 '23 at 16:53

2 Answers2

1

A good smooth transition is obtained with the function

$$ t(x,\lambda,x_0) = \frac{\ln (\cosh (\lambda (x-x_0)))}{2 \lambda }-\frac{\lambda x_0-\ln (2)}{2 \lambda }+\frac{x}{2} $$

This function is obtained integrating

$$ \frac{1}{2} (\tanh (\lambda (x-x_0))+1) $$

as

$$ \int_x \frac{1}{2} (\tanh (\lambda (x-x_0))+1)dx=\frac{\ln (\cosh (\lambda (x-x_0)))}{2 \lambda }+\frac{x}{2}+c_0 $$

and then calculating $c_0$ as

$$ \lim_{x\to-\infty}\frac{\ln (\cosh (\lambda (x-x_0)))}{2 \lambda }+\frac{x}{2}+c_0=0 $$

enter image description here

NOTE

With $x_0$ the transition is located at a precise point. If $x_0=0$ and $\lambda=2$ we have

$$ t(x) = \frac{\ln (\cosh (2 x))}{4 }+\frac{\ln (2)}{4 }+\frac{x}{2} $$

Cesareo
  • 33,252
  • Thanks for commenting. I believe your answer is more suitable to this question, since I was asking on how approximate the mentioned integral. Now tbh, I think the comment by @RaymondManzoni wins every other answer because of its simplicity as a smooth transition function: $x/(1-e^{-8x})$ – Joako Jul 19 '23 at 16:37
  • now I retracted, I just found the mentioned smooth transition is not exactly zero for negative values of $x$. – Joako Jul 19 '23 at 16:52
1

Though not quite a standard power series, one can derive the series representation

$$g(x)=\int\limits_{-1}^x \frac{1}{e^{\frac{4 u}{u^2-1}}+1} \, du= \frac{x+1}{2}+\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{a_n}{2 n} \left(x^{2 n}-1\right)\right),\quad -1<x<1\tag{1}$$

from the Maclaurin series

$$f(u)=\frac{1}{e^{\frac{4 u}{u^2-1}}+1}=\frac{1}{2}+\underset{N\to\infty}{\text{lim}}\left(\sum_{n=1}^N a_n u^{2 n-1}\right),\quad -1<u<1 \tag{2}$$

where $a_n=\frac{f^{(2n-1)}(0)}{(2 n-1)!}$ via term-wise integration, i.e. $\int\limits_{-1}^x \frac{1}{2} \, du=\frac{x+1}{2}$ and $\int\limits_{-1}^x a_n u^{2n-1} \, du=\frac{a_n}{2 n} \left(x^{2 n}-1\right)$.

The first few terms of the series for $f(u)$ are

$$f(u)=\frac{1}{2}+u-\frac{u^3}{3}-\frac{13 u^5}{15}+\frac{67 u^7}{315}+\frac{3083 u^9}{2835}...\tag{3}$$

and the first few terms of the series for $g(x)$ are

$$g(x)=\frac{x+1}{2}+\frac{x^2-1}{2}-\frac{x^4-1}{12}-\frac{13 \left(x^6-1\right)}{90}+\frac{67 \left(x^8-1\right)}{2520}+\frac{3083 \left(x^{10}-1\right)}{28350}..\tag{4}.$$

Figure (1) below illustrates $f(u)=\frac{1}{e^{\frac{4 u}{u^2-1}}+1}$ in blue and the Maclaurin Series for $f(x)$ in orange where the series defined in formula (2) above is evaluated at $N=100$.

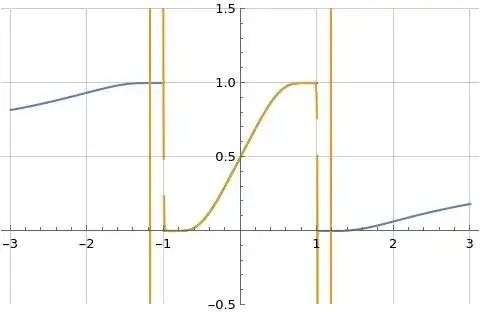
Illustration of f(u)

Figure (1): Illustration of $f(u)=\frac{1}{e^{\frac{4 u}{u^2-1}}+1}$ (blue) and associated Maclaurin series (orange)

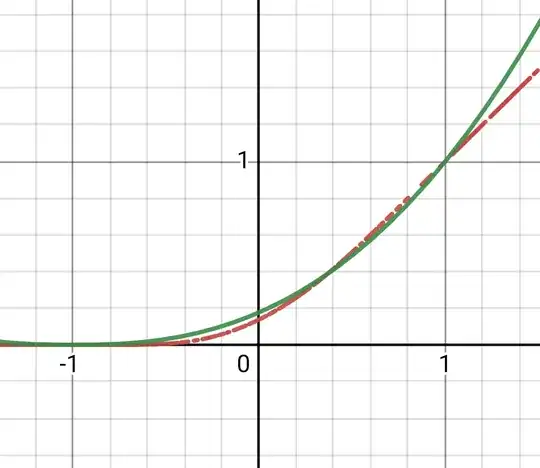
Figure (2) below illustrates $g(x)=\int\limits_{-1}^x \frac{1}{e^{\frac{4 u}{u^2-1}}+1} \, du$ in blue and the series for $g(x)$ in orange where the integral in formula (1) above is evaluated using numerical integration (via Mathematica's NIntegrate function) and the series defined in formula (1) above is evaluated at $N=100$.

Illustration of g(x)

Figure (2): Illustration of $g(x)=\int\limits_{-1}^x \frac{1}{e^{\frac{4 u}{u^2-1}}+1} \, du$ (blue) and associated series (orange)

One can also derive the Maclaurin series

$$g(x)=\int\limits_{-1}^x \frac{1}{e^{\frac{4 u}{u^2-1}}+1} \, du=b+\frac{x}{2}+\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{a_n}{2 n}\, x^{2 n}\right),\quad -1<x<1\tag{5}$$

where

$$b=\int\limits_{-1}^0 \frac{1}{e^{\frac{4 u}{u^2-1}}+1} \, du\approx 0.137775\tag{6}$$

and $a_n$ is the same as in formulas (1) and (2) above.

The first few terms of the Maclaurin series for $g(x)$ defined in formula (5) above are

$$g(x)=b+\frac{x}{2}+\frac{x^2}{2}-\frac{x^4}{12}-\frac{13 x^6}{90}+\frac{67 x^8}{2520}+\frac{3083 x^{10}}{28350}...\tag{7}$$

Figure (3) below illustrates $g(x)=\int\limits_{-1}^x \frac{1}{e^{\frac{4 u}{u^2-1}}+1} \, du$ in blue and the Maclaurin series for $g(x)$ defined in formula (5) above in orange where the integral in formula (5) above is evaluated using numerical integration and the Maclaurin series defined in formula (5) above is evaluated at $N=100$.

Illustration of formula (5) for g(x)

Figure (3): Illustration of $g(x)=\int\limits_{-1}^x \frac{1}{e^{\frac{4 u}{u^2-1}}+1} \, du$ (blue) and formula (5) Maclaurin series (orange)

Steven Clark
  • 7,363
  • Thanks for answering. I have a few questions: Those coefficients $a_n$ are the same for the series of $g(x)$ and $f(u)$?; Could be any of the coefficients' series shown in Wolfram-Alpha be used as the $a_n$s for $f(x)$?; It is possible to display explicetely the formula of the coefficients $a_n(n)$? (this will solve both previous questions) – Joako Jul 19 '23 at 19:01
  • 1
    @Joako Yes the values of $a_n$ in formulas (1) and (2) are identical, and the first few values are $\left{1,-\frac{1}{3},-\frac{13}{15},\frac{67}{315},\frac{3083}{2835},\frac{41617}{155925},-\frac{5993633}{6081075},-\frac{441300421}{638512875},\frac{6982395467}{10854718875},\frac{1575917664301}{1856156927625}\right}$ which I evaluated with the Mathematica SeriesCoefficient function, but the general relationship is $a_n=\frac{f^{(2n-1)}(0)}{(2 n-1)!}$ where $f(u)=\frac{1}{e^{\frac{4 u}{u^2-1}}+1}$. – Steven Clark Jul 19 '23 at 19:34
  • Can I ask you 2 another favors?: Could you confirm the first terms of the expansion are this ones?; The other one, Could you upload also Figure 1 but on an interval were also its shown how the expansions fails to fit? (don't know, maybe $[-5,\ 5]$ or wider). Thanks beforehand. – Joako Jul 19 '23 at 20:55
  • I am trying to work with the series but its hard to find the terms $a_n=\frac{f^{(2n-1)}(0)}{(2n-1)!}$.. It is possible to relate them somehow with the "easier" coefficients shown in Wolfram-Alpha?: $$\dfrac{1}{1+\exp\left(\dfrac{4x}{x^2-1}\right)}=\dfrac{1}{1+\sum\limits_{n=0}^\infty \dfrac{\left(\frac{4x}{x^2-1}\right)^n}{n!}}$$ – Joako Jul 19 '23 at 23:19
  • Also I just figure out that if I ask Wolfram-Alpha by the indefinite integral it indeed gives a taylor expansion, that missed the curve only by a contant given by the term $\int_{-1}^0 f(u)\ du \approx 0.13775$ as shown in Wolfram-Alpha, which could be seen in Desmos. But I don't have any clue about which formula those coefficients have. – Joako Jul 19 '23 at 23:56
  • 1
    I updated my answer to address the questions in your first follow-on comment. In your second follow-on comment, the expansion in the WolframAlpha link about $x=0$ is equivalent to formula (3) in my updated answer above, whereas the other series formula with the sum in the denominator is based on the Maclaurin series for $e^x$ about $x=0$, and seems to be more relatable to $$f(u)=\frac{1}{e^{\frac{4 u}{u^2-1}}+1}=\sum\limits {m=0}^{\infty} (-1)^m, e^{m \frac{4 u}{u^2-1}}=\sum\limits{m=0}^{\infty} (-1)^m \sum\limits_{n=0}^{\infty} \frac{\left(m \frac{4 u}{u^2-1}\right)^n}{n!}.$$ – Steven Clark Jul 20 '23 at 03:39
  • 1
    I'll take a look at your third follow-on comment above when I have more time. – Steven Clark Jul 20 '23 at 03:43
  • thanks you very much. By inspection I guess that the sum of all the constant values that came from the "ones" on the terms $\text{coeff}n\cdot (x^{2n}\pm 1)$ of the series of $g(x)$ should be equal to the constant value $\int{-1}^0 \frac{1}{1+\exp(4x/(x^2-1))}dx$... that is my guess. I hope it is so the series could be reduced in complexity. – Joako Jul 20 '23 at 04:19
  • 1
    @Joako I added the definition and illustration of the Maclaurin series for $g(x)$ to my answer above. Comparing formulas (1) and (5) for $g(x)$ does seem to suggest $$b=\int\limits_{-1}^0 \frac{1}{e^{\frac{4 u}{u^2-1}}+1} , du=\frac{1}{2}-\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{a_n}{2 n}\right)\approx 0.137775$$. – Steven Clark Jul 20 '23 at 15:25