I need an infinitely smooth non-decreasing function $\ f(x)$, that $$f(x)=0\quad\forall x\leq 0,$$ $$f(x)=1\quad\forall x\geq 1,$$ and all its derivatives in $x=0$ and $x=1$ are $0$.
I found that I can't present any such function, what makes me confused. I know many examples of smooth finite hat-function, such as $e^{1/{(x-1)x}}$, but I still can't make it useful to create that step.
Recall that $$f(t) = \left\{ \begin{array}{lr} e^{-1/t} & t >0\\ 0 & t \leq 0\\ \end{array}\right.$$ is smooth. Then $g(t) = \frac{f(t)}{f(t)+f(1-t)}$ is smooth, is equal to $1$ for $t \geq 1$, and equal to $0$ for $t \leq 0$.
This is the standard construction; you can probably find it in most any intro book to smooth manifolds, for instance, in their discussion on bump functions.
My version of step-smooth function with infinite count of zero derivatives is
\begin{align} f(x) = \begin{cases} 0& x\leq 0\\ \frac{1}{2} \left(\tanh \left(\frac{k (2 x-1)}{2 \sqrt{(1-x) x}}\right)+1\right)& 0<x<1 \\1 & x\geq 1\end{cases} \end{align}
where $k$ is derivative at $x=1/2$.
How about using the Standardmollifier and massage it a bit:
\begin{align} f(x) = \begin{cases} 0& \text{ if } x\leq 0\\ e^{1+\frac{-1}{1-(x-1)^2}}& \text{ if }0<x<1 \\1 & \text{ if }x\geq 1\end{cases} \end{align}
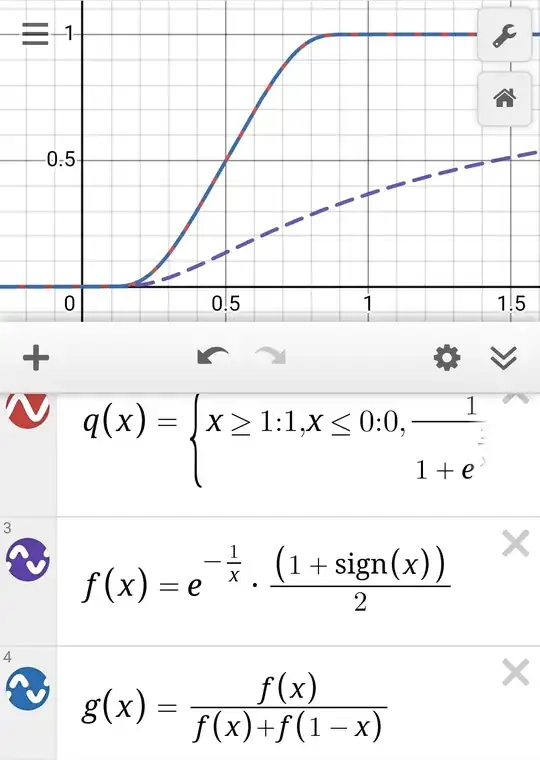
Following the answer by @user98602, you could use as example a piecewise version of the function $\frac{1}{1+\exp((2x-1)/(x^2-x))}$, which details could be found in this question I did: $$r(x)=\dfrac{1}{1+\exp\left(\dfrac{2x-1}{x^2-x}\right)\dfrac{\left(1+\text{sgn}(1-x)\right)}{\left(1+\text{sgn}(x)\right)}}$$
will make the trick, in principle. But caution must be taken since as could be seen the function $r(x)$ is undefined at the points $x=\{0,\ 1\}$ (something similar happened in this question), so to keep smoothness a piecewise definition is mandatory: $$q(x)=\begin{cases}0,\quad x\leq 0\\ 1,\quad x\geq 1\\ \dfrac{1}{1+\exp\left(\dfrac{2x-1}{x^2-x}\right)},\ \text{otherwise} \end{cases}$$
Also be aware that since this function behave as flat function so by its nature is an example of non-analytic smooth functions, as also are smooth bump functions (this is why I edit one of your original tags).
You could see these functions in Desmos:
