I have two functions $f(x)$ and $g(x)$, and I am looking for a continuous function $h(x)$, or rather $\hat{h}(x)$, which smoothly transitions from $f$ to $g$ over a fixed interval $[x_0,x_1]$, i.e.
$$h(x)=\begin{cases}f(x), &x \le x_0\\ \hat{h}(x), &x_0 < x < x_1\\ g(x) ,& x_1 \le x\end{cases}$$
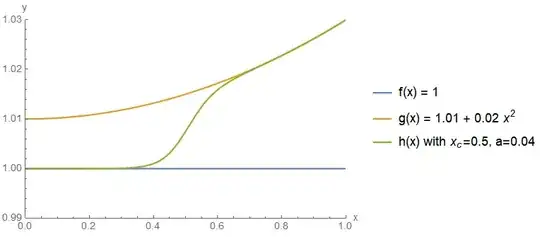
On here https://kitchingroup.cheme.cmu.edu/blog/2013/02/27/Smooth-transitions-between-two-constants I found the example of $$h(x) \ =\ f(x) \ +\ \Big(g(x)-f(x)\Big) \cdot \left(1 - \frac{1}{1 + \exp\{-(x_c-x)/a\}}\right)$$
which gives e.g.
This is a very nice transition function, but the problem with this approach is that there is only one center point $x_c$. That is, the transition is not perfectly bound between two points $x_0$ and $x_1$, but rather converges to $0$ as we move away from $x_c$.
Can this idea be tweaked to support a fixed transition interval $[x_0,x_1]$?