3

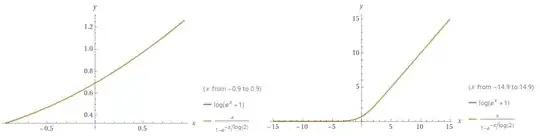
Consider $\alpha = \log a$ and $\beta = \log b$, $b>a$. Are there formulas for approximating $\gamma = \log (a+b)$? What about $\theta = \log (a-b)$?

If it makes it easier, assume that $|\alpha| \gg 300$ so the obvious solution $\gamma = \log (10^\alpha + 10^\beta)$ is infeasible using standard double-precision floating point arithmetic (you can't easily store $a$ and $b$ in memory to begin with!).

Hari
  • 239
badp
  • 1,256

2 Answers2

2

Working in other question I found that for positive $x,y$ you could approximate: $$\ln(x+y)\approx \begin{cases} \frac{x^{\frac{1}{\ln(2)}}\ln(x)-y^{\frac{1}{\ln(2)}}\ln(y)}{x^{\frac{1}{\ln(2)}}-y^{\frac{1}{\ln(2)}}}, \quad x\neq y\\ \ln(x)+\ln(2),\quad x=y \end{cases}$$

which is based in this other approximation: $$\ln(1+e^x) \approx \begin{cases} \frac{x}{1-e^{-\frac{x}{\ln(2)}}},\quad x\neq 0\\ \ln(2),\quad x=0\end{cases}$$

For the last one the maximum error is below $0.0092$, and the plot is quite close:

comparison of the plots

Joako
  • 1,380
  • 1
    What do you mean quite close, it's almost exact! +1 – Kamal Saleh Jan 06 '24 at 03:50
  • 1
    quite and almost are words that sometimes let you in trouble in this site lol. If $x+y\to 0$ you could have issues since $\ln(x)$ "explodes" to negative infinite faster: plot the relation for $x$ with $y=1$ and you will see it... for very small $x$ the logarithm is better approximated by $\ln(x)\approx \frac{1-x^{-x}}{x}$ – Joako Jan 06 '24 at 04:37
2

you can try this here $\gamma=\log\left[a\left(1+\frac{b}{a}\right)\right]$= $\log(a)+\log\left(1+\frac{b}{a}\right)$

Dr. Sonnhard Graubner
  • 95,283
  • which, if $\beta$ is much larger than $\alpha$, then $\log(1 + \frac{b}{a})$ is approximately $\log(\frac{b}{a}) = \log(b) - log(a)$ and the entire thing degrades to approximately $log(b)$. – Irvan Oct 10 '14 at 16:02
  • 2
    Since $b>a$, a better approximation would be $\log b+\log(1+a/b)\approx\log b+(a/b)=\beta+\exp(\alpha-\beta)$. –  Oct 10 '14 at 16:30
  • @Rahul Wait, is $\log(1+\frac ab) \simeq \frac a b$?! That sounds... very strange. – badp Oct 10 '14 at 17:22