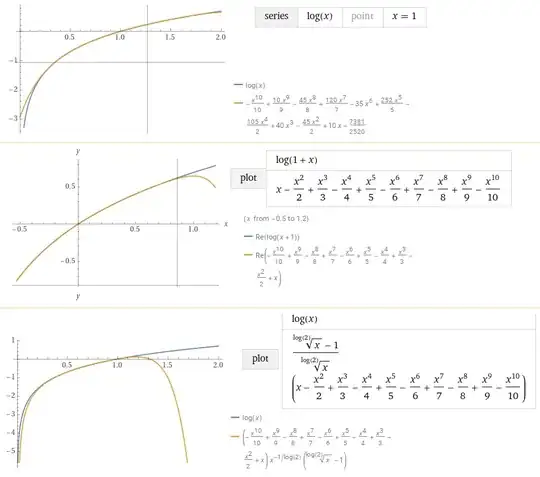
To avoid the $\log()$ function, I am looking for a good approximation of $\log(x)$ for very small $x$ (e.g. order $10^{-5}$).
I think Taylor series expansion is useless because around these small $x$, the first order derivative approachs $+\infty$.
I did try this approximation $\log_{10}(x) \approx 1 - \frac{1}{\sqrt{x}}$ but still don't have satisfactory results.
Could anyone suggest some better approximations?