Recapitulating the question with just a little extra notation,
we have two real functions
$$f(z) = \mathrm{Re}\left(\frac{1}{1+z^2}\right)$$
and
$$g(z) = \mathrm{Im}\left(\frac{1}{1+z^2}\right).$$
Taking $z = x + iy,$
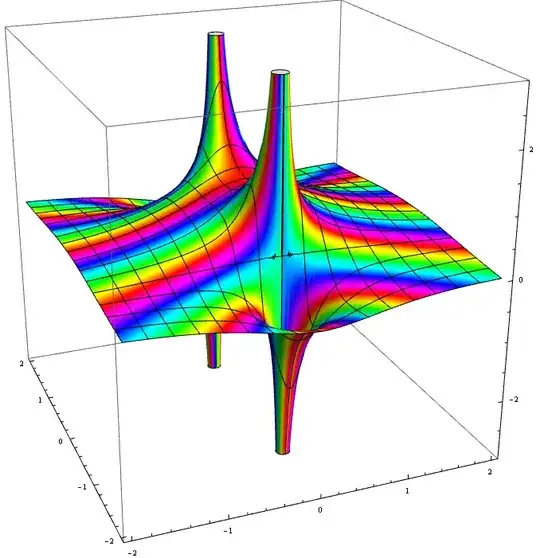
we can plot one of these functions (for example, $f$) in three dimensions
by labeling the three axes $x,$ $y,$ and $w$ (using $w$ for the third axis since we've already used $z$ for something else)
and plotting the equation
$$ w = f(x + iy).$$
Now we want to "slice" this plot along one of the planes through the
origin perpendicular to the $x,y$ plane,
that is, we want a slice along a plane containing the $w$-axis,
but rotated an angle $\theta$ away from the $x$-axis.
Because complex analysis is involved here,
let's measure $\theta$ in radians rather than degrees.
(This will simplify some formulas later.)
We might as well assume $\theta \in [0, \pi),$at least for now,
because every other angle will slice the three-dimensional graph
along one of the planes described by $\theta \in [0, \pi).$
This slice can then be viewed as a graph in two dimensions.
Naturally, we might expect to be able to impose a Cartesian coordinate system on this plane so that we can write an equation for the graph.
Since the $w$ axis already lies in the plane, it is an obvious candidate
for one of the coordinate axes of the slice.
In order to form a Cartesian coordinate system that describes the slice
in the usual way (mapping equations to shapes in the way we usually expect),
the other coordinate axis of the slice should be perpendicular to the
$w$-axis, and the unit of measurement along that axis should be equal to
the unit along the $w$-axis.
That is, we want to set up a coordinate axis along the line
$y = x\tan\theta$ in the $x,y$ plane;
and if we call this the $u$-axis, then we want the point
$(u,w) = (1,0)$ in the plane of the slice to be the point
$(x,y,w) = (\cos\theta, \sin\theta, 0).$
In order to evaluate $f(z)$ (or $g(z)$) at any given value of $u,$ we
can write $z = u\cos\theta + iu \sin\theta,$
or more simply, $z = u e^{i\theta}.$
Observing that $\bar z = u e^{-i\theta},$ we have
\begin{align}
\frac{1}{1+z^2}
&= \frac{1}{1+u^2 e^{i2\theta}} \\
&= \frac{1}{1+u^2 e^{i2\theta}}
\cdot\frac{1+u^2 e^{-i2\theta}}{1+u^2 e^{-i2\theta}} \\
&= \frac{1+u^2 e^{-i2\theta}}
{1+u^2 (e^{-i2\theta} + e^{-i2\theta}) + e^{i2\theta}e^{-i2\theta} u^4}\\
&= \frac{1+(\cos(2\theta))u^2 - i(\sin(2\theta))u^2}
{1+(2\cos(2\theta))u^2 + u^4}\\
\end{align}
and therefore
$$
f(z) = \mathrm{Re}\left(\frac{1}{1+z^2}\right)
= \frac{1+(\cos(2\theta))u^2}{1+(2\cos(2\theta))u^2 + u^4}
$$
and
$$
g(z) = \mathrm{Im}\left(\frac{1}{1+z^2}\right)
= \frac{-(\sin(2\theta))u^2}{1+(2\cos(2\theta))u^2 + u^4}
$$
We can now relax our constraints on $\theta$; if we let
$\theta$ be any real number, the angles $\theta_1$ and
$\theta_2 = \theta_1 - \pi$
both specify the same slice of the three-dimensional graph,
except that the $u$-axis for $\theta_1 - \pi$ runs in the opposite
direction from the $u$-axis for $\theta_1.$
If you just pick angles randomly then you will almost certainly end
up with transcendental coefficients in these equations;
but if you simply set either $\cos\theta$ or $\sin\theta$
to a rational number between $-1$ and $1$ and apply the usual
trigonometric identities, you will get relatively reasonable coefficients
(rational numbers and/or square roots of rational numbers).
Examples
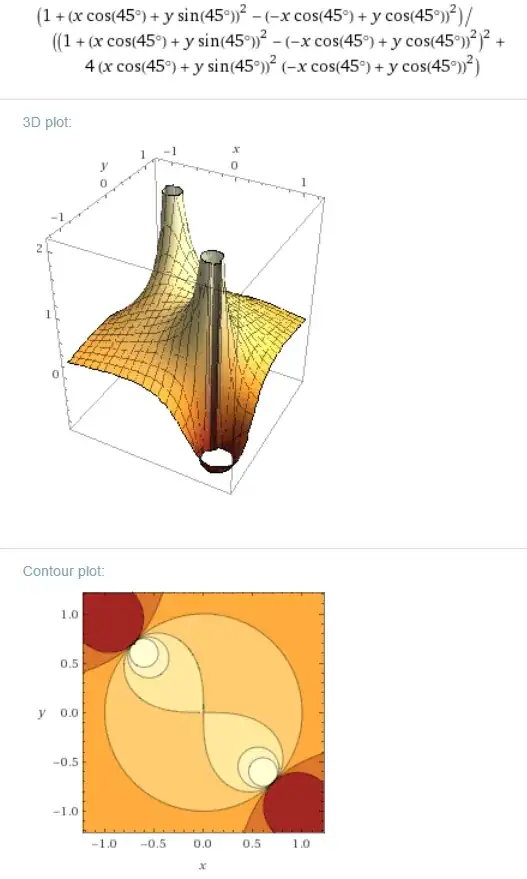
The table below shows the functions we obtain by “slicing” the graph of $\frac1{1+z^2}$ at a few different angles:
$\theta=0$ (slicing along the $x$ axis), $\theta=\frac\pi4$ radians ($45$ degrees, slicing along the line $y=x$), and $\theta=\frac\pi2$ ($90$ degrees, slicing along the $y$ axis).
\begin{array}{ccccccccc}
\theta&\ &\cos(2\theta)&\ &\sin(2\theta)&\ &\mathrm{Re}\left(\dfrac{1}{1+z^2}\right)&\ & \mathrm{Im}\left(\dfrac{1}{1+z^2}\right) \\
\hline
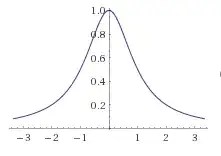
0 && 1&& 0 && \dfrac{1+u^2}{1+2u^2+u^4} = \dfrac{1}{1+u^2} && 0\\
\frac\pi4&& 0&& 1 && \dfrac{1}{1+u^4} && \dfrac{-u^2}{1+u^4} \\
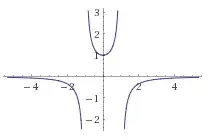
\frac\pi2&&-1&& 0 && \dfrac{1-u^2}{1-2u^2+u^4} = \dfrac{1}{1-u^2} && 0\\
\end{array}
Alternatives
In general, if you write $z = x + iy,$ then $f(z)$ and $g(z)$ can also be written as functions of the real and imaginary components of $z$:
\begin{align}
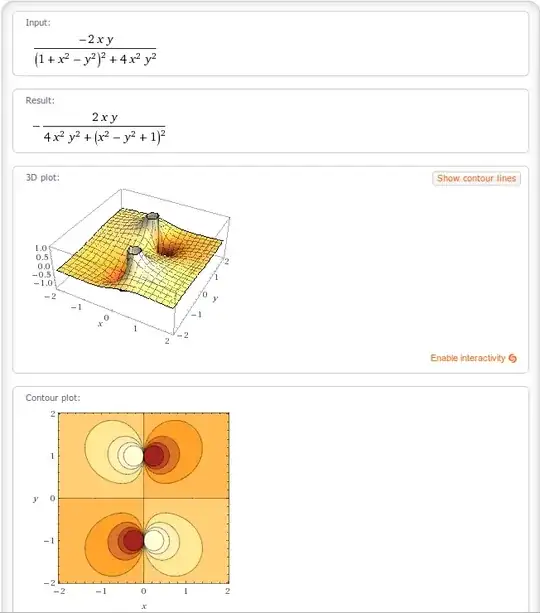
f(x, y) &= f(x + iy) = \frac{1+x^2-y^2}{(1+x^2-y^2)^2+4x^2y^2}, \\
g(x, y) &= g(x + iy) = \frac{-2xy}{(1+x^2-y^2)^2+4x^2y^2}.
\end{align}
A "slice through the origin" gives a line in the complex plane with
an equation like the following in $x$ and $y$:
$$ Ax + By = 0,$$
where $A$ and $B$ are not both zero.
Take $A = 0$ and you have the equation of the $x$-axis;
take $B = 0$ and you have the $y$-axis;
take $A = \tan\theta$ and $B = -1$ and you have a line rotated by an angle
$\theta$ from the $x$-axis, with slope $m = \tan\theta$
and equivalent equation $y = mx.$
Note that after you "split" $z$ into real and imaginary components
$x$ and $y,$ you generally require both components in order to
evaluate $f$ and $g$ at any value $z.$
If you simply erase $y$ from the formula for $f$ above, you end up with
$\frac{1+x^2}{(1+x^2)^2+4x^2},$ which you can easily verify is
not a faithful formula for $\mathrm{Re}\left(\frac{1}{1+z^2}\right).$
On the other hand, if you "slice" a function such as $f(x,y)$ along a line
through the origin, you have something that resembles a function of
one (real-valued) coordinate plotted in a plane,
that is, a single-parameter real function.
There should be a way to write $f$ as such a function.
Any resolution to this question is going to come down to choosing
one real-valued variable as an independent coordinate, and using some
functions of that variable as the $x$ and $y$ values in $f(x,y).$
In the question, one method is explored in which we set
$f(x,y) = f(x, x\tan\theta).$ That is, we use $x$ for $x$ itself and
$x\tan\theta$ for $y.$
This makes it possible to plot $f$ as a function of $x$ along along any line
whose equation can be written $y = x\tan\theta.$
It is not possible to plot $f$ in this way along the $y$ axis.
Another method is to set $f(x,y) = f(y\cot\theta, y).$
This makes it possible to plot $f$ as a function of $y$ along along any line
whose equation can be written $x = y\cot\theta,$
that is, along any line through the origin except the $x$-axis.
You can use the second method to describe the slice of $f$ along the $y$-axis
as a single-parameter real function,
and the first method to describe any other slice of $f$ through the origin.
If you apply this method along lines at angles near $90$ degrees
(but not at $90$ degrees exactly),
you can observe that the function increases from $1$ toward a maximum value,
then falls to a negative minimum value, then increases asymptotically to zero;
as the angle of the line approaches $90$ degrees, the maximum and minimum
values get more extreme and also occur at $x$-values closer and closer to zero.
At $90$ degrees exactly, the function increases to infinity and then from
negative infinity back up to zero, which is consistent with the trend of the
other functions, but rather than doing this at an input value of zero
(to which the extreme points of the other functions were converging),
it does this at the input value $1.$
Alternatively, you can use the first method just to describe the slice of $f$
along the $x$-axis, and use the second method for the other slices.
This gives quite different results (most of the time) compared to the
previous paragraph, but the results are just as valid.
Yet another alternative is to set $f(x,y) = f(x, x\tan\theta)$
when slicing along any line up to $45$ degrees from the $x$-axis
(that is, any line $y = mx$ where $-1 \leq m \leq 1)$,
and set $f(x,y) = f(y\cot\theta, y)$ when slicing at any other angle.
A nice thing about this is that the two methods match up perfectly
along the lines $y = x$ and $y = -x,$ which are the lines at exactly
the angles where we switch from one method to the other.
The method I described above is just another method for reducing $f$
to a single-parameter real function.
In that method, we set $f(x,y) = f(u\cos\theta, u\sin\theta).$
Along a line at angle $\theta$ from the $x$-axis,
where $\theta$ is a constant,
this reduces $f$ to a function of the real variable $u.$
It can also be viewed as using polar coordinates to describe points
in the complex plane, with $u$ as the radius from the origin.
The formulas I gave for $f(z)$ and $g(z)$ in terms of $u$ are just
what you get if you substitute $x = u\cos\theta$ and $y = u\sin\theta$
in the formulas for $f(x,y)$ and $g(x,y).$
(Note that then $x^2 - y^2 = u^2 \cos(2\theta)$ and $2xy = u^2 \sin(2\theta).$)
And these are merely a few of the infinite number of alternative methods.
You can take your pick or come up with another that you prefer.
Appendix
Here are some reasons why I personally prefer the method I described in the first part of this answer,
writing $z = u\cos\theta + i u\sin\theta.$
In general, except when $\theta = 0$ the
$x$-axis does not actually lie in the slice taken through the origin.
In effect, the method of setting $f(z) = f(x, x\tan\theta)$
is a projection of the $x$-axis onto the plane of the slice
(or vice versa).
The projection is parallel to the $y$-axis, so when
$\theta$ is near $\frac\pi2,$ that is, when the slice is nearly parallel
to the $y$-axis, the projection onto the slice is "stretched"
in the horizontal direction.
This can have some weird results.
For example, consider the plot of the real function $h(z) = |z|^2.$
The graph $w = h(x+iy)$ is a paraboloid of revolution around the $w$-axis,
that is, every slice is a parabola of the same shape.
But if we take the slice at $\theta = \frac32$
(that is, rotated about $85.94$ degrees from the $x$-axis),
and plot $w$ as a function of $x$ in that slice,
we find that in this slice,
$$
w = \left|x + i\tan\left(\tfrac32\right)\right|^2
= \left(\sec^2\left(\tfrac32\right)\right) x^2
\approx 199.85 x^2,
$$
although in the slice for $\theta = 0$ the equation is $w = x^2.$
How can two slices have such different equations
when they have the same shape?
The answer is that we have used an unnatural, distorted coordinate system
for the slice at $\theta = \frac32.$
This coordinate system works weirdly in that slice.
(And as we know, it doesn't work at all in the slice $\theta = \frac\pi2.$)
If you set up a $u$-axis in the slice, however, then no matter what
value of $\theta$ you use you will always find that the equation
of the slice is $w = u^2,$ which describes the actual
shape of the slice in the way we usually expect.
And when $\theta = \frac\pi2,$ then $u = y,$
so we end up using the $y$ axis instead of the $x$ axis
just as in the other answer.

\Re(z)for $\Re(z)$ or\operatorname{Re}(z)for $\operatorname{Re}(z)$ – gen-ℤ ready to perish Nov 18 '17 at 23:49