1

Graphing the real part of complex function $\frac{1}{1+z^2}$ colored according to the imaginary part yields:

$$Re(\frac{1}{(1+z^2)})=\frac{1+x^2-y^2}{(1+x^2-y^2)^2+4x^2y^2}$$

$$Im(\frac{1}{(1+z^2)})=\frac{-2xyi}{(1+x^2-y^2)^2+4x^2y^2}$$

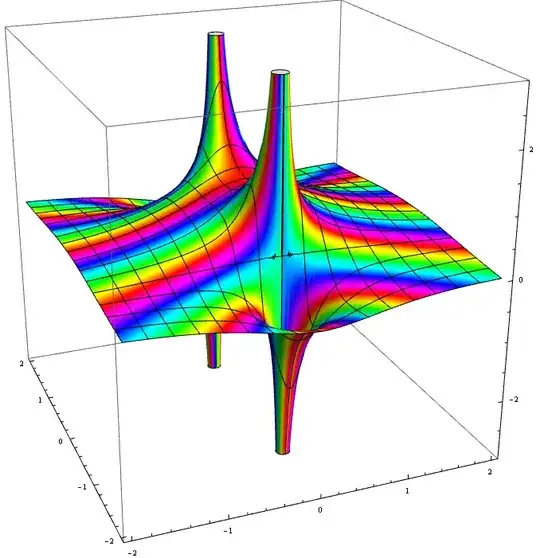
enter image description here

Slicing the graph of the real components with a plane rotated by $θ$ about the z-axis is possible as demonstrated by DanielFisher Here: "set $y=c⋅x$ where $c=tan(θ)$ and $θ$ is the angle between the vertical plane and the positive real axis. $y=c⋅x=tan(θ)$."

$$Re(\frac{1}{(1+z^2)})=\frac{1+x^2-y^2}{(1+x^2-y^2)^2+4x^2y^2}$$

replacing the y with $tan(\theta)\cdot x$:

$$\frac{1+x^2-(tan(\theta)*x)^2}{(1+x^2-(tan(\theta)*x)^2)^2+4x^2(tan(\theta)*x)^2}$$

Setting $\theta=45$ reduces to a nice clean Cartesian equation:

$$\frac{1+x^2-(tan(45)*x)^2}{(1+x^2-(tan(45)*x)^2)^2+4x^2(tan(45)*x)^2}=\frac{1}{4x^2+1}$$

This is a follow up question to that one:

How can the axis of rotation for the slicing plane be separated from the origin? How can the angle of the axis of rotation for the slicing plane be made skew relative to the z-axis?

Community
  • 1
User3910
  • 2,390

1 Answers1

0

I asked this question over at Reddit, and got some useful responses.

To get a horizontal plane slice parallel to the x-y plane, merely set the equation equal to an integer value equal to the desired height.

To quote CZeke from reddit: "If you're interested in the slice above the line y=mx+b, sub that in for y. You'll get z in terms of x alone, and that's what the slice looks like. (It will be stretched horizontally by a factor of something like m/√(1+m2), but that's true of slices through the origin too.)"

User3910
  • 2,390