Following this guide to Sage: and using Sage Online produced the following graphs:
Graphing $\frac{1}{1-z}$ that way yeilds:
Graphing $\frac{1}{1-z^2}$ that way yields:
It would be nice to see it in 3D instead of merely color coded. The y-axis is coming out of the picture toward us and instead of seeing the 3D surface (in x,y,i coordinates) we see a color-graph on the x-i plane.
This is the codes in which you can visualize the complex functions in Maple's environment:
[> with(plots):
[> f := z-> 1/(1-z):
g:=z-> 1/(1-z^2):
[> complexplot3d(f, -2-2*I .. 2+2*I);
complexplot3d(g, -2-2*I .. 2+2*I);
To the best of my knowledge, Sage at present does not offer 3d plots with color determined by a function. (But I'm not a Sage expert like those who inhabit ask Sage Q&A site.) As Babak S. pointed out, Maple does the job, for those who have access to it. However, I think the following picture (made with a different Maple command) looks nicer:
f:=1/(1-(x+I*y)^2):
plot3d(abs(f), x=-3..3, y=-3..3, color=argument(f), grid=[50,50]);
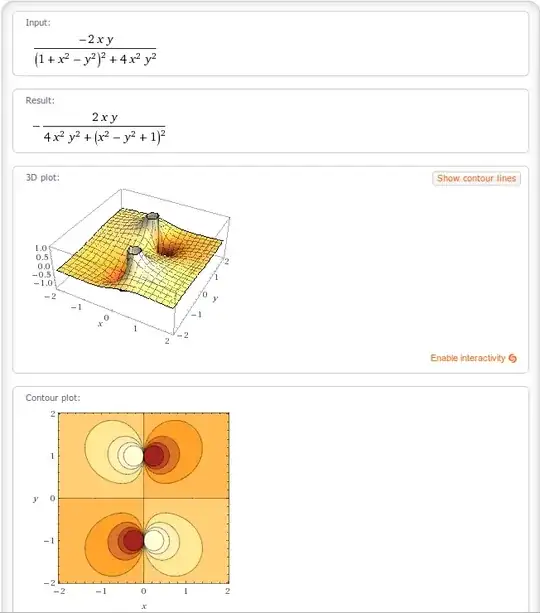
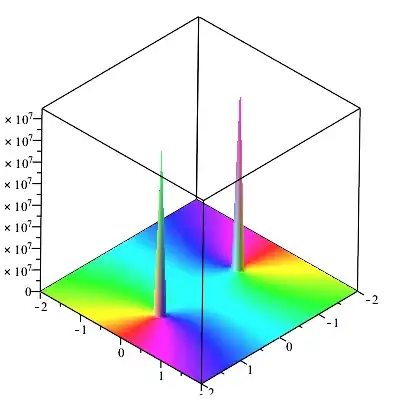
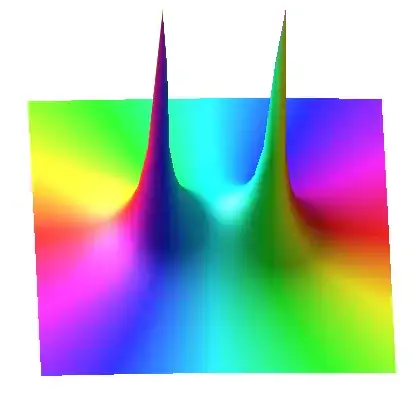
You can understand complex functions better by expanding in terms of real variables. For example, let's take a look at the function $$\frac{1}{1+z^2}$$ by letting $z=x+iy$, where $x$ and $y$ are real. Then $$\frac{1}{1+(x+iy)^2}=\frac{1}{1+x^2-y^2+2xyi}=\frac{1+x^2-y^2-2xyi}{(1+x^2-y^2)^2+4x^2y^2},$$ where we have multiplied numerator and denominator of the middle expression by the complex conjugate of the denominator to make the denominator purely real. You can then separate to obtain $$\frac{1}{1+z^2}=\frac{1+x^2-y^2}{(1+x^2-y^2)^2+4x^2y^2}-i\frac{2xy}{(1+x^2-y^2)^2+4x^2y^2}.$$
Notice how the complex function is broken into real and imaginary components.
$$\text{Re}\left(\frac{1}{1+z^2}\right)=\frac{1+x^2-y^2}{(1+x^2-y^2)^2+4x^2y^2}$$
$$\text{Im}\left(\frac{1}{1+z^2}\right)=\frac{-2xy}{(1+x^2-y^2)^2+4x^2y^2}$$
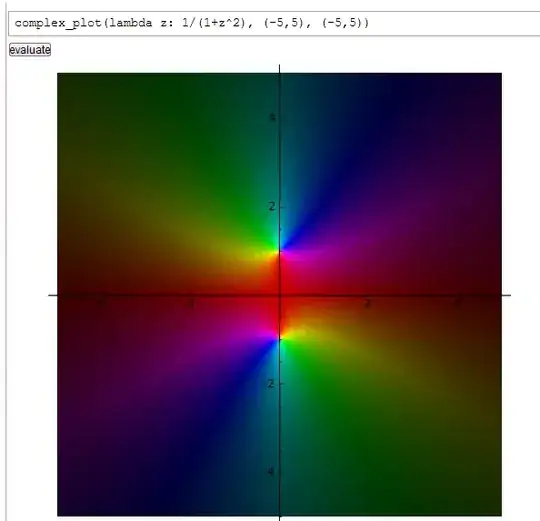
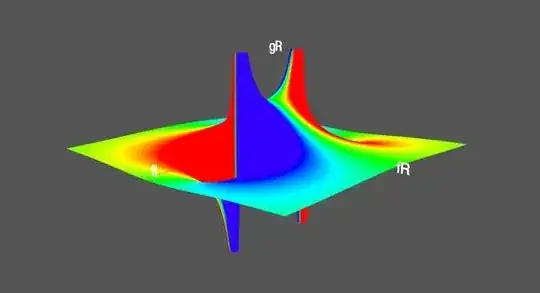
ADDED BY OTHER USER: AntonioVargas shared the following plot from Mathematica of $\text{Re}(1/(1+z^2))$ colored according to $\text{Im}(1/(1+z^2))$:
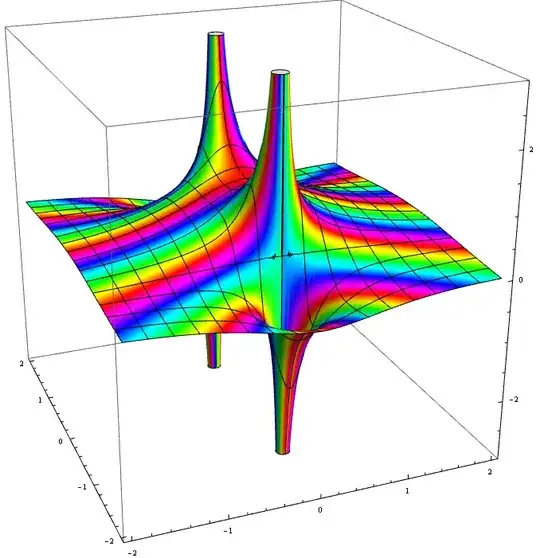
However it is just as easy to graph it in Wolfram Alpha
The graph the Re(1/(1+z^2) on Wolfram Alpha!
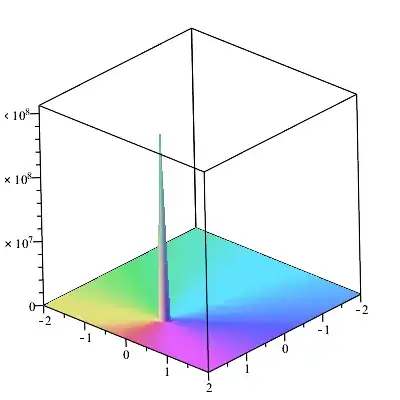
Also the 3D plot of the imaginary component.
I wrote a little something in three.js/webgl to do this.
It allows you to choose how to map your 4 available complex axes to X,Y,Z and color gradient.
It is using math.js, so to express formulas you need to call the appropriate math.js functions which isn't so elegant, but it works. E.g. for
$$ \frac{1}{1+z^2} $$
you write:
g=divide(1,add(1,pow(f,2)))
Free, no install of anything required. Sharable. Just a hobby project, but might be useful. Some other examples here.
The simplest way is to merely replace z with "x+iy" and hit enter in wolfram alpha:
$$ 1/(1+(x+iy)^2)$$
or for 1/(1-(x+iy)^2)
1/(1-x^2+y^2-2xyi) times