How Relate Complex and Cartesian Functions For $\frac{1}{1+z^2}$, $\frac{1}{1-x^2}$, and $\frac{1}{1+x^2}$

Question

This question is clumsily phrased: please ignore it and instead see the improved version here.

The graph of $$\frac{1}{1+z^2}$$ is:

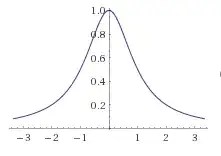
enter image description here

The graph of $$\frac{1}{1+x^2}$$ is:

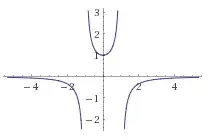
enter image description here

And the graph of $$\frac{1}{1-x^2}$$ Is:

enter image description here

And the graph of $$\left|\frac{1}{1-x^2}\right|$$ Is:

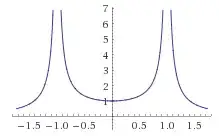
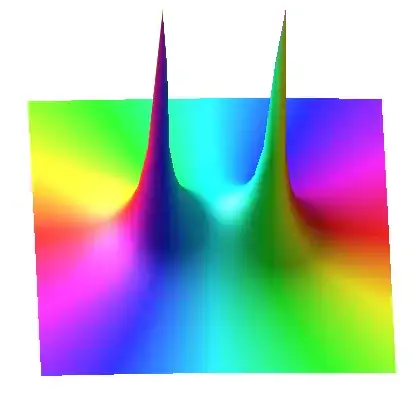
enter image description here

Notice how the graph of $\frac{1}{1+x^2}$ is equivalent to cutting the complex graph with a vertical plane directly between the two singularities (along the real axis). Notice also how cutting the complex graph with a vertical plane throug the two singualrites (perpendicular to the real axis) yeilds $|\frac{1}{1-x^2}|$. Obviously the complex plane and the cartesian plane bear some relation that it somewhat baffeling:

1.) Why must $\frac{1}{1-x^2}$ have it's absolute value taken before matching the complex function $\frac{1}{1+z^2}$?

2.) Graphing $\frac{1}{1-z^2}$ instead of $\frac{1}{1+z^2}$ rotates the singularities from $0,\pm i$ to $\pm 1, 0i$ or rotates the complex into the real and the real into the complex, but the same cartesian graphs apply. This suggests that what is on the real axis and what is on the imaginary axis is arbitrary because in one case the graph $\frac{1}{1+x^2}$ corresponds to the the vertical slice along the real axis and in the other case it corresponds to the vertical slice along the imaginary axis. The point of saying it is arbitrary is that $\frac{1}{1+x^2}$ is no more real or imaginary than $\frac{1}{1-x^2}$. Is that a valid conclusion?

3.) Is it possible to write a cartesian equation equivalent to a vertical plane through the complex plane $\frac{1}{1+z^2}$ for every possible angle and not just perpendicular or parallel to the real axis? If yes, how?

[edit]

AntonioVargas shared the following plot of $Re(1/(1+z^2))$ colored according to $Im(1/(1+z^2))$:

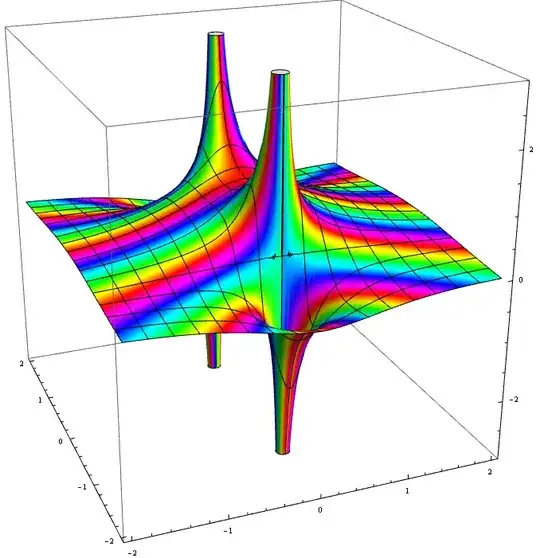
enter image description here

This plot explains why the Absolute value was necessary for the Cartesian function to represent the Complex function: The complex function had its absolute value taken as well. Questions 2 & 3 remain open.

[edit 2]

Thanks to pbs for finally explaining how to graph a complex function! I was able to graph the Re(1/(1+z^2) on Wolfram Alpha!

enter image description here

However the 3D plot of the imaginary component begs more questions than it answers:

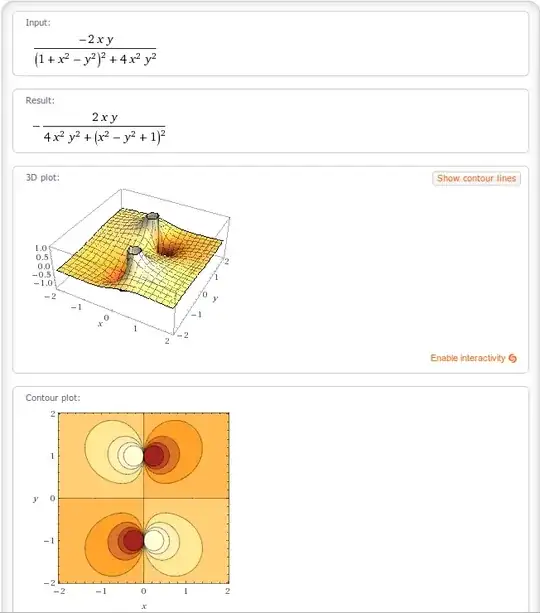
enter image description here

It would be so much simpler to explain with out the Imaginary plot! What's going on here? The absolute value seems to have been taken without having been stated. Hmmmm... Back to question 1 as unanswered! (except this time only for $Im(1/(1+z))$.

Think about what you mean by 'the graph of' a holomorphic function. — Rhys, Aug 07 '13 at 15:04
The height of your graph of $1/(1+z^2)$ is $|1/(1+z^2)|$ and it is colored according to $\arg 1/(1+z^2)$. — Antonio Vargas, Aug 07 '13 at 15:09
@AntonioVargas Is there a way to graph it 3D without the absolute values? — User3910, Aug 07 '13 at 22:43
You could plot $\operatorname{Re}\Bigl(1/(1+z^2)\Bigr)$ and color it according to $\operatorname{Im}\Bigl(1/(1+z^2)\Bigr)$ as in this image. — Antonio Vargas, Aug 07 '13 at 23:36
The answers to this question have revealed to me that this question is clumily phrased and so I am asking a cleaned up version here. — User3910, Aug 08 '13 at 22:40

score 2 · Answer 1 · edited Aug 07 '13 at 21:22

2

The singluarities of $\frac{1}{1+z^2}$ are at plus/minus i...

Consider $z = (1 + c)i, e > 0$

Then,

$$\frac{1}{1+z^2} = \frac{1}{1 - (1 + c)^2} < 0$$

So you're first graph is wrong... the graph should become negative near the singularities

edited Aug 07 '13 at 21:22

User3910

2,390

answered Aug 07 '13 at 16:44

Jonathan Viccary

241

Welcome to MSE! It really helps readability to format answers using MathJax (see FAQ). Regards – Amzoti Aug 07 '13 at 17:03
Technically it is the graph of $\frac{1}{1-z^2}$, but I don't have maple or mathematica and Sage only does 2D graphs. – User3910 Aug 07 '13 at 21:26

score 2 · Accepted Answer · answered Aug 08 '13 at 08:20

2

You can understand complex functions better by expanding in terms of real variables. For example, expand $$\frac{1}{1+z^2}$$ by letting $z=x+iy$. Then $$\frac{1}{1+(x+iy)^2}=\frac{1}{1+x^2-y^2+2xyi}=\frac{1+x^2-y^2-2xyi}{(1+x^2-y^2)^2+4x^2y^2}.$$ You can then separate to obtain $$\frac{1}{1+z^2}=\frac{1+x^2-y^2}{(1+x^2-y^2)^2+4x^2y^2}-i\frac{2xy}{(1+x^2-y^2)^2+4x^2y^2}.$$ Investigating this will help you to compare the complex function with your alternative real function more precisely.

answered Aug 08 '13 at 08:20

pshmath0

10,565

I'm a little confused what you did between $1/1+x^2...$ and $1+x^2..../()^2+4x^2 y^2$. – User3910 Aug 08 '13 at 08:27
Multiply the numerator and denominator by the conjugate of the denominator, e.g. if the fraction were $$\frac{1}{u+iv}$$ then you would multiply numerator and denominator by $u-iv$, thus $$\frac{u-iv}{(u+iv)(u-iv)}.$$ This is perfectly valid since we are just multiplying by $1$ in "disguise". We call $u-iv$ the complex conjugate of $u+iv$. This is the method we use to make a complex denominator of a fraction purely real. – pshmath0 Aug 08 '13 at 08:28
Thankyou soooo much for explaining how to graph complex function!!!!! I have tried for a lllloooonnnggg time to figure that out! Everyone is like "buy Maple/Mathematica" or quit. If you wouldn't mind copying and pasting the answer over here I will gladly make it the accepted answer there. – User3910 Aug 08 '13 at 08:41
You're welcome. – pshmath0 Aug 10 '13 at 14:06

How Relate Complex and Cartesian Functions For $\frac{1}{1+z^2}$, $\frac{1}{1-x^2}$, and $\frac{1}{1+x^2}$

2 Answers2