How to match my curve with the correct lemniscate?

Question

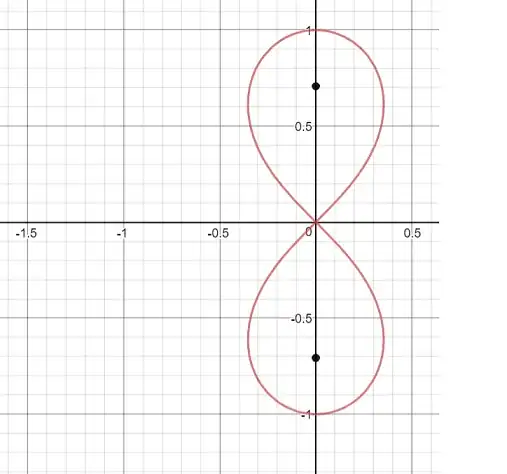
$$\frac{1+x^2-y^2}{(1+x^2-y^2)^2+4x^2y^2}=1$$ appears to be a lemniscate. However, there are many different types: https://en.wikipedia.org/wiki/Lemniscate How to match my curve with the correct leminscate?

Answer 1

Your equation is equivalent to $$x^4 + 2 x^2 y^2 + y^4+ (x^2 - y^2)=0$$ so is a Bernoulli lemniscate with equation $$(x^2+y^2)^2=2a^2 (x^2-y^2)$$ ( with $x$,$y$ switched) where $2 a^2 = 1$,$a= \frac{1}{\sqrt{2}}$.

Answer 2

Just simplifying the given equation of $\cal C$ you have $$(x^2+y^2)^2=y^2-x^2.......(1)$$ The focus of $\cal C$ being $F_1=(0,a)$ and $F_2=(0,-a)$ we have for $P=(x,y)\in\cal C$

$$a^2=PF_1\cdot PF_2=\sqrt{(x^2+y^2)^2+2a^2(x^2-y^2)+a^4}$$ equivalently $$(x^2+y^2)^2=2a^2(y^2-x^2).......(2)$$ Taking the point $(0,1)\in\cal C$ we have $2a^2=1$ so $(1)$ and $(2)$ coincide and consequently $\cal C$ is a Bernoulli's lemniscata with focus $\left(0,\pm\dfrac{\sqrt2}{2}\right)$.