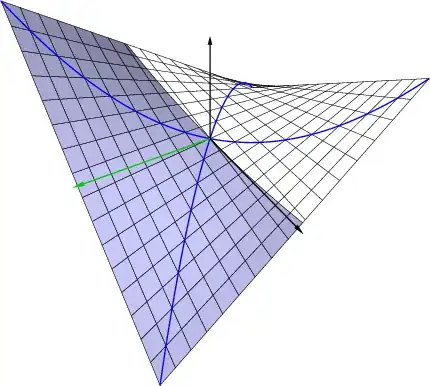
I can find slices of a surface for any angle through the vertical axis, but I am not certain what the equation of the surface is.
Equation along x-axis: $z=1/(1+x^2)$
Equation along y-axis:$z=1/(1-y^2)$
Equation at 45 degrees: $z=1/(t^4+1)$, where t is the line in the x-y plane at 45 degrees.
Equation at 30 degrees: $z=1/((9/4*t^2)+1)$, where t is the line in the x-y plane at 30 degrees.
Feel free to ask for the equation of a slice through any angle. What is the equation of the surface?