Evaluating $\lim\limits_{x\to \infty}\sqrt[6]{x^{6}+x^{5}}-\sqrt[6]{x^{6}-x^{5}}$

Question

How would you evaluate the following limit: $$\lim_{x\to \infty}\sqrt[6]{x^{6}+x^{5}}-\sqrt[6]{x^{6}-x^{5}}$$

I tried to use this formula: $a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})$, It didn't work.

Any hints?

Answer 1

So many clever solutions, so many convenient algebraic manipulations to remember... For those of us with small-sized memories, let us come back to plain analysis. The method is automatic, it requires zero idea and it wins.

To wit, the main term in $x^6\pm x^5$ is $x^6$ hence $\sqrt[6]{x^6\pm x^5}=x+o(x)$. Oops... this only gives that the difference is $(x+o(x))-(x+o(x))=o(x)$, but we are after the limit so $o(x)$ is not enough, not even to show that the limit exists. We must go (at least) one step further in the expansions, so let us do that.

Note first that, if $u=o(1)$, then $\sqrt[6]{1+u}=1+\frac16u+o(u)$ because $(1+u)^a=1+au+o(u)$ for every $a$ and because $\sqrt[6]{1+u}=(1+u)^{1/6}$.

Furthermore, $\sqrt[6]{x^6\pm x^5}=x\sqrt[6]{1\pm u}$ with $u=\frac1x$, hence $\sqrt[6]{x^6\pm x^5}=x\left(1\pm\frac16u+o(u)\right)$, that is, $\sqrt[6]{x^6\pm x^5}=x\pm\frac16+o(1)$.

This proves that the difference is $(x+\frac16+o(1))-(x-\frac16+o(1))=\frac13+o(1)$, in other words the limit exists and is $\frac13$. End of the proof.

Corollary: Consider some positive real numbers $n$ and $m$, real numbers $\alpha$ and $\beta$, and functions $A$ and $B$ such that $A(x)$ is $o(x^{n-1})$ and $B(x)$ is $o(x^{m-1})$. Then, $$ \lim_{x\to+\infty}\color{red}{\sqrt[n]{x^n+\alpha x^{n-1}+A(x)}-\sqrt[m]{x^m+\beta x^{m-1}+B(x)}}=\color{red}{\frac{\alpha}n-\frac{\beta}m}. $$

Answer 2

Hint: See this FAQ page. One way to apply what was done there directly is rewrite your limit as $$\lim_{x\to \infty}\left(\sqrt[6]{x^{6}+x^{5}}-x\right)- \lim_{x\rightarrow\infty}\left(\sqrt[6]{x^{6}-x^{5}}-x\right).$$ In any case, take a look at what was done, because the ideas used on that thread will solve your problem.

Hope that helps,

Answer 3

Hint: use $a^6 - b^6 = (a - b)(a^5 + a^4 b + a^3 b^2 + a^2 b^3 + a b^4 + b^5)$ with $a =(x^6 + x^5)^{1/6} = x (1 + 1/x)^{1/6}$ and $b = (x^6 - x^5)^{1/6} = x (1 - 1/x)^{1/6}$.

Answer 4

Edit: The main idea is to use the expansion

$$\sqrt[6]{1+x^{-1}}=1+\frac{1}{6}x^{-1}+O\left( x^{-2}\right) $$

which can be generated by changing variables $x=1/z$, expanding about $z=0$, $$\sqrt[6]{1+z}=1+\frac{1}{6}z+O\left( z^{2}\right) $$ and restoring $x$ via $% z\rightarrow 1/x$.

---

Let $f(x)=\sqrt[6]{x^{6}+x^{5}}-\sqrt[6]{x^{6}-x^{5}}$. If $\lim_{x\rightarrow +\infty }(x)=L$, then $\lim_{x\rightarrow -\infty }f(x)=-L$ because $f(-x)=-f(x)$. We have

$$f(x) =\sqrt[6]{x^{6}+x^{5}}-\sqrt[6]{x^{6}-x^{5}}=\left\vert x\right\vert \left( \sqrt[6]{1+x^{-1}}-\sqrt[6]{1-x^{-1}}\right). $$

Since

$$\sqrt[6]{1+x^{-1}} =1+\frac{1}{6}x^{-1}+O\left( x^{-2}\right)\quad\text{ and }\quad\sqrt[6]{1-x^{-1}} =1-\frac{1}{6}x^{-1}+O\left( x^{-2}\right),$$

we get

$$\sqrt[6]{1+x^{-1}}-\sqrt[6]{1-x^{-1}}=\frac{1}{3}x^{-1}+O\left( x^{-2}\right)$$

and for $x>0$

$$x\left( \sqrt[6]{1+x^{-1}}-\sqrt[6]{1-x^{-1}}\right) =\frac{1}{3}+O\left( x^{-1}\right).$$

Therefore

$$L=\lim_{x\rightarrow +\infty }f(x) =\lim_{x\rightarrow +\infty }\left\vert x\right\vert \left( \sqrt[6]{1+x^{-1}}-\sqrt[6]{1-x^{-1}}\right)=\lim_{x\rightarrow +\infty }\frac{1}{3}+O\left( x^{-1}\right) =\frac{1}{3}.$$

---

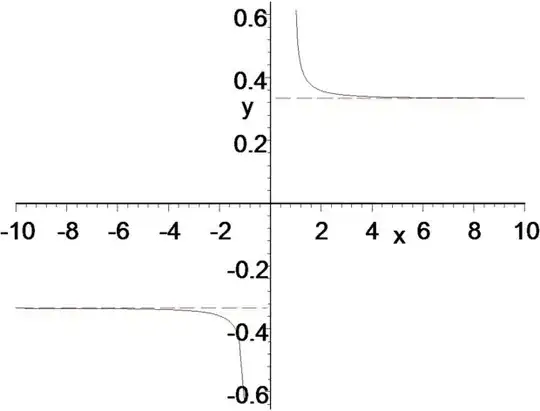
Edit 2: graph of $f(x)$

Answer 5

$$ \begin{aligned} \lim _{x\to \infty }\left(\sqrt[6]{x^6+x^5}-\sqrt[6]{x^6-x^5}\right) & = \lim _{t\to 0}\left(\sqrt[6]{\frac{1}{t^6}+\frac{1}{t^5}}-\sqrt[6]{\frac{1}{t^6}-\frac{1}{t^5}}\right) \\& = \lim _{t\to 0}\left(\left(\sqrt[6]{\frac{1}{t^6}+\frac{1}{t^5}}-\sqrt[6]{\frac{1}{t^6}-\frac{1}{t^5}}\right)\cdot \frac{\left(\sqrt[6]{\frac{1}{t^6}+\frac{1}{t^5}}+\sqrt[6]{\frac{1}{t^6}-\frac{1}{t^5}}\right)}{\sqrt[6]{\frac{1}{t^6}+\frac{1}{t^5}}+\sqrt[6]{\frac{1}{t^6}-\frac{1}{t^5}}}\right) \\& = \lim _{t\to 0}\left(\frac{\sqrt[3]{t+1}-\sqrt[3]{-t+1}}{t\left(\sqrt[6]{-t+1}+\sqrt[6]{t+1}\right)}\right) \\& = \lim _{t\to 0}\left(\frac{\left(1+\frac{1}{3}t+o\left(t\right)\right)-\left(1-\frac{1}{3}t+o\left(t\right)\right)}{t\left(2+o\left(1\right)\right)}\right) \\& = \color{red}{\frac{1}{3}} \end{aligned} $$

Solved with substitution $t=\frac{1}{x}$ and Taylor expansion