To sum $1+2+3+\cdots$ to $-\frac1{12}$

Question

$$\sum_{n=1}^\infty\frac1{n^s}$$ only converges to $\zeta(s)$ if $\text{Re}(s)>1$.

Why should analytically continuing to $\zeta(-1)$ give the right answer?

Answer 1

there are many ways to see that your result is the right one. What does the right one mean?

It means that whenever such a sum appears anywhere in physics - I explicitly emphasize that not just in string theory, also in experimentally doable measurements of the Casimir force (between parallel metals resulting from quantized standing electromagnetic waves in between) - and one knows that the result is finite, the only possible finite part of the result that may be consistent with other symmetries of the problem (and that is actually confirmed experimentally whenever it is possible) is equal to $-1/12$.

It's another widespread misconception (see all the incorrect comments right below your question) that the zeta-function regularization is the only way how to calculate the proper value. Let me show a completely different calculation - one that is a homework exercise in Joe Polchinski's "String Theory" textbook.

Exponential regulator method

Add an exponentially decreasing regulator to make the sum convergent - so that the sum becomes $$ S = \sum_{n=1}^{\infty} n e^{-\epsilon n} $$ Note that this is not equivalent to generalizing the sum to the zeta-function. In the zeta-function, the $n$ is the base that is exponentiated to the $s$th power. Here, the regulator has $n$ in the exponent. Obviously, the original sum of natural numbers is obtained in the $\epsilon\to 0$ limit of the formula for $S$. In physics, $\epsilon$ would be viewed as a kind of "minimum distance" that can be resolved.

The sum above may be exactly evaluated and the result is (use Mathematica if you don't want to do it yourself, but you can do it yourself) $$ S = \frac{e^\epsilon}{(e^\epsilon-1)^2} $$ We will only need some Laurent expansion around $\epsilon = 0$. $$ S = \frac{1+\epsilon+\epsilon^2/2 + O(\epsilon^3)}{(\epsilon+\epsilon^2/2+\epsilon^3/6+O(\epsilon^4))^2} $$ We have $$ S = \frac{1}{\epsilon^2} \frac{1+\epsilon+\epsilon^2/2+O(\epsilon^3)}{(1+\epsilon/2+\epsilon^2/6+O(\epsilon^3))^2} $$ You see that the $1/\epsilon^2$ leading divergence survives and the next subleading term cancels. The resulting expansion may be calculated with this Mathematica command
1/epsilon^2 * Series[epsilon^2 Sum[n Exp[-n epsilon], {n, 1, Infinity}], {epsilon, 0, 5}]

and the result is $$ \frac{1}{\epsilon^2} - \frac{1}{12} + \frac{\epsilon^2}{240} + O(\epsilon^4) $$ In the $\epsilon\to 0$ limit we were interested in, the $\epsilon^2/240$ term as well as the smaller ones go to zero and may be erased. The leading divergence $1/\epsilon^2$ may be and must be canceled by a local counterterm - a vacuum energy term. This is true for the Casimir effect in electromagnetism (in this case, the cancelled pole may be interpreted as the sum of the zero-point energies in the case that no metals were bounding the region), zero-point energies in string theory, and everywhere else. The cancellation of the leading divergence is needed for physics to be finite - but one may guarantee that the counterterm won't affect the finite term, $-1/12$, which is the correct result of the sum.

In physics applications, $\epsilon$ would be dimensionful and its different powers are sharply separated and may be treated individually. That's why the local counterterms may eliminate the leading divergence but don't affect the finite part. That's also why you couldn't have used a more complex regulator, like $\exp(-(\epsilon+\epsilon^2)n)$.

There are many other, apparently inequivalent ways to compute the right value of the sum. It is not just the zeta function.

Euler's method

Let me present one more, slightly less modern, method that was used by Leonhard Euler to calculate that the sum of natural numbers is $-1/12$. It's of course a bit more heuristic but his heuristic approach showed that he had a good intuition and the derivation could be turned into a modern physics derivation, too.

We will work with two sums, $$ S = 1+2+3+4+5+\dots, \quad T = 1-2+3-4+5-\dots $$ Extrapolating the geometric and similar sums to the divergent (and, in this case, marginally divergent) domain of values of $x$, the expression $T$ may be summed according to the Taylor expansion $$ \frac{1}{(1+x)^2} = 1 - 2x + 3x^2 -4x^3 + \dots $$ Substitute $x=1$ to see that $T=+1/4$. The value of $S$ is easily calculated now: $$ T = (1+2+3+\dots) - 2\times (2+4+6+\dots) = (1+2+3+\dots) (1 - 4) = -3S$$ so $S=-T/3=-1/12$.

A zeta-function calculation

A somewhat unusual calculation of $\zeta(-1)=-1/12$ of mine may be found in the Pictures of Yellows Roses, a Czech student journal. The website no longer works, although a working snapshot of the original website is still available through the WebArchive (see this link). A 2014 English text with the same evaluation at the end can be found at The Reference Frame.

The comments were in Czech but the equations represent bulk of the language that really matters, so the Czech comments shouldn't be a problem. A new argument (subscript) $s$ is added to the zeta function. The new function is the old zeta function for $s=0$ and for $s=1$, it only differs by one. We Taylor expand around $s=0$ to get to $s=1$ and we find out that only a finite number of terms survives if the main argument $x$ is a non-positive integer. The resulting recursive relations for the zeta function allow us to compute the values of the zeta-function at integers smaller than $1$, and prove that the function vanishes at negative even values of $x$.

Answer 2

Here is a variant on Lubos Motl's answer:

Let $S = \sum_{n=1}^{\infty} n$. Then $S - 4 S = \sum_{n = 1}^{\infty} (-1)^{n-1} n.$ We will evaluate this latter expression with a regularization similar to Lubos Motl's.

Namely, consider $$\sum_{n=1}^{\infty} (-1)^{n-1} n t^n = -t \dfrac{d}{dt} \sum_{n=1}^{\infty} (-t)^n = -t \dfrac{d}{dt} \dfrac{1}{1+t} = \dfrac{t}{(1+t)^2}.$$
Letting $t \to 1,$ we find that $-3 S = \dfrac{1}{4}$, and hence that $S = \dfrac{-1}{12}.$

---

To see the relationship between this approach and Lubos Motl's, note that if we write $t = e^{\epsilon},$ then $t\dfrac{d}{dt} = \dfrac{d}{d\epsilon},$ so in fact the arguments are essentially the same, except that Lubos doesn't perform the initial step of replacing $S$ by $S - 4S$, which means that he has the pole $\dfrac{1}{\epsilon^2}$ which he then subtracts away.

---

As far as I know, this trick of replacing $\zeta(s)$ by $(1-2^{-s+1})^{-1}\zeta(s)$ is due to Euler, and it is a now standard method for replacing $\zeta(s)$ by a function which carries the same information, but does not have a pole at $s = 1$. The evaluation of $\zeta(s)$ at negative integers by passing to $(1-2^{-s+1})\zeta(s)$ and then performing Abelian regularization as above is also due to Euler, I believe. It is easy to see the Bernoulli numbers appearing in this way, for example.

---

Of course, taken literally, the series $\sum_{n=1}^{\infty} n$ diverges to $+\infty$, so any attempt to assign it a finite value will involve some form of regularization. Analytic continuation of the $\zeta$-function is one form of regularization, and the Abelian regularization that Lubos Motl and I are making is another. I can't quote a precise theorem to this effect (although maybe others can), but with such a simple expression as $\sum_{n = 1}^{\infty} n,$ I'm reasonably confident that any sensible regularization will necessarily yield the same value of $\dfrac{-1}{12}$. (Lubos Motl makes the same assertion in his answer.)

Answer 3

What a great method! I tried a few... $$ \sum_{n = 1}^{\infty} \left(\frac{1}{(2 n)^{s}} - \frac{1}{(2 n - 1)^{s}}\right) = \zeta (s) \Bigl(2^{1 - s} - 1\Bigr) $$ put $s=-1$ to get $\sum_{n = 1}^{\infty} 1 = -\frac{1}{4}$

or $$ \sum_{n = 1}^{\infty} \left(\frac{1}{(2 n + 1)^{s}} - \frac{1}{(2 n)^{s}}\right) = \left(1 - 2^{1-s}\right)\zeta(s) - 1 $$ put $s=-1$ to get $\sum_{n = 1}^{\infty} 1 = -\frac{3}{4}$

Answer 4

Computation of $\boldsymbol{\zeta(-1)}$ Using Integration by Parts

Here is a direct computation of $\zeta(-1)$ taken from this answer:

Multiply equation $(1)$ from this answer by $x+1$, then integrate by parts twice, to get $$ \begin{align} (1-2^{1-x})\zeta(x)\Gamma(x+2) &=\int_0^\infty\frac{(x+1)xt^{x-1}}{e^t+1}\mathrm{d}t\\ &=\int_0^\infty\frac{(x+1)t^xe^t}{(e^t+1)^2}\mathrm{d}t\\ &=\int_0^\infty\frac{t^{x+1}(e^{2t}-e^t)}{(e^t+1)^3}\mathrm{d}t\tag{1} \end{align} $$ Now we can plug in $x=-1$ into $(1)$ to get $$ \begin{align} (1-2^2)\zeta(-1)\Gamma(1) &=\int_0^\infty\frac{e^{2t}-e^t}{(e^t+1)^3}\mathrm{d}t\\ &=\int_1^\infty\frac{u-1}{(u+1)^3}\mathrm{d}u\\ &=\int_1^\infty\left(\frac1{(u+1)^2}-\frac2{(u+1)^3}\right)\mathrm{d}u\\ &=\frac14\tag{2} \end{align} $$ Since $(1-2^2)\Gamma(1)=-3$, $(2)$ says that $$ \zeta(-1)=-\frac1{12}\tag{3} $$ Naively plugging $n=-1$ into $$ \zeta(n)=\frac1{1^n}+\frac1{2^n}+\frac1{3^n}+\dots\tag{4} $$ yields $$ -\frac1{12}=1+2+3+4+\dots\tag{5} $$ However, the series on the right of $(5)$ is obviously divergent by the Term Test.

---

Computation of $\boldsymbol{\zeta(-1)}$ Using Euler-Maclaurin Sum Formula

As is shown in $(10)$ from this answer, for $\mathrm{Re}(s)\lt3$, we have $$ \lim_{n\to\infty}\left(\sum_{k=1}^nk^s-\frac{n^{s+1}}{s+1}-\frac{n^s}2-\frac{s\,n^{s-1}}{12}\right)=\zeta(-s)\tag6 $$ Plugging in $s=1$, we get $$ \begin{align} \zeta(-1) &=\lim_{n\to\infty}\overbrace{\left(\sum_{k=1}^nk-\frac{n^2}2-\frac{n}2-\frac1{12}\right)}^{-\frac1{12}\text{ for all $n$}}\\ &=-\frac1{12}\tag7 \end{align} $$

Answer 5

[19/3/19] Update - ref. 3b1b - Visualizing the Riemann hypothesis and analytic continuation : https://youtu.be/sD0NjbwqlYw - this piece demonstrates utmost clarity on $\zeta(-1)$ evaluation.

---

:: An explanation of how this is true and why and where it is useful and significant is summarized in 24 by John Baez (as part of the 19/09/08 Rankin Lectures) and yes, indeed this is weird.

---

The following is the same Euler's method described by Luboš Motl and Matt E in the other answers.

Let us consider the infinite geometric progression " $1, x, x^2, x^3, x^4, \dots$ "

The sum of this progression can be found by the formula $S_\infty = \large \frac{a}{1-r}$,

$$\implies 1 + x + x^2 + x^3 + x^4 + \dots = \frac{1}{1-x}$$ Differentiating with respect to $x$, $$ \implies 0 + 1 + 2x + 3x^2 + 4x^3 + \dots = \frac{1}{(x-1)^2}$$ Let $x = -1$, (Note: In the LHS, you get the alternating counterpart of the natural numbers series) $$\implies 1-2+3-4+5-6+...= \frac{1}{4} $$

$$ \bbox[5px,border:2px solid green]{\therefore \sum\limits_{i=1}^\infty n(-1)^{n-1} = \frac{1}{4}} $$

Subtracting this from $\sum\limits_{i=1}^\infty n$, $$\sum\limits_{i=1}^\infty n -\sum\limits_{i=1}^\infty n(-1)^{n-1} =4+8+12+...=4\sum\limits_{i=1}^\infty n$$ $$\implies 3\sum\limits_{i=1}^\infty n =-\sum\limits_{i=1}^\infty n(-1)^{n-1}=-1/4$$ $$\bbox[5px,border:2px solid lime]{\therefore \sum\limits_{i=1}^\infty n=-\frac{1}{12}}$$

---

This intuitive reasoning was made famous in a video by the physicist Phil Plait of Numberphile. It is heavily criticized for being sloppy but it shows a simple method that has fooled a large population of its high school audience (as noted in the comments).

---

Funfact: Googling -1/12 doesn't give you any results

Answer 6

This infinite series is ultimately divergent because $$ 1+2+3+4+\cdots=\sum\limits_{k=1}^{\infty} k$$ $$ = \lim\limits_{n\to\infty} \sum\limits_{k=1}^{n} k = \lim\limits_{n\to\infty} \frac{n(n+1)}{2} = \infty $$ The value of $-\frac{1}{12}$ is attained by applying a different summability method, such as zeta function regularization and several others. If you'd like to understand how a divergent series can report a finite value by applying a different summability method, then have a look at this question.

Answer 7

If the following were true: $$\sum_{n=1}^\infty{n}=-\frac1{12}\tag{hypothesis}$$ then we would expect the following: $$\lim_{n\to\infty}\sum_{i=1}^n{i}\\ =\lim_{n\to\infty}\frac{n(n+1)}2=-\frac1{12}\tag{expectation}$$ which is the formula for the infinite triangular number limit. Unfortunately this is a result that we do not get when the limit is correctly taken. The correct value is $$\lim_{n\to\infty}\frac{n(n+1)}{2}\\ =\lim_{n\to\infty}\frac{n^2+n}{2}\\ =\lim_{m:{n^2+n}\to\infty}\frac{m}{2}=\infty\\ \neq-\frac{1}{12}$$ This sort of mathematical sleight of hand, smoke and mirrors, pulling a finite negative rabbit out of an empty positively infinite hat does not impress me; worse yet, it gives legitimate, observable, repeatable mathematics a bad name.

Answer 8

The notation "$1+2+3+\cdots$" is as meaningless as "$1/0$". If you treat such notation as though it defined a real number and conformed in its syntax to the rules of formation for genuine real numbers, you can easily "prove" it to equal any number you like, including $-1/12$.

Answer 9

I am missing here that

$$1+2+3+\cdots \rightarrow \infty$$

$$\zeta(-1) \neq 1+2+3+\cdots$$

As you say, we only define $\zeta$ using the infinite sum if $\Re(s)>1$.

---

It is just as defining $$f(x) = \begin{cases} \frac{1}{x} &\mathrm{if} \; x \neq 0 \\ 0 & \mathrm{if} \; x = 0 \end{cases}$$

And asking why $f(0)=0$.

Answer 10

A nice alternative representation, by a double sum.

Consider the infinite square array where the rowsums and the (formal) column-sums are also given in closed forms $$ \small \begin{array} {r|rrrrr|rr} & & & & & & \text{rowsums} \\ \hline & 1/0! & \log(1)/1! & \log(1)^2/2! &\log(1)^3/3! & \cdots & = e^{\log(1)}&=1 \\ & 1/0! & \log(2)/1! & \log(2)^2/2! &\log(2)^3/3! & \cdots & = e^{\log(2)}&=2 \\ & 1/0! & \log(3)/1! & \log(3)^2/2! &\log(3)^3/3! & \cdots & = e^{\log(3)}&=3 \\ & \vdots & & & & \ddots & \vdots & \vdots\\ \hline \text{colsums:} & \zeta(0) & -\zeta(0)'/1! & \zeta(0)''/2!& -\zeta(0)^{(3)}/3! & \cdots &&=\zeta(-1) \end{array} $$ and the row-sum of the derivatives of the $\zeta()$ at $0$ in the bottom row can numerically be written as $$ \small -0.5 +0.9189... -1.003178...+1.000785...-0.999879...+1.0000019... \pm \cdots $$ If we split the terms and do two series we find $$ \Tiny \begin{array} {} -1 &+1 &-1 &+1 &-1 &+1 &\pm &\cdots &=-1/2\\ +0.5 &-0.0810... &-0.003178...&+0.000785...&+0.000120...&+0.0000019... &\pm &\cdots &= 5/12\\ \end{array}$$ Here we must now resort to the earlier definition of the divergent sum of the alternating units (in the first row), but the second row is convergent and can conventionally be summed. The sum of the two rowsums $\small -1/2 + 5/12 = -1/12$ gives the expected result.

However, that fiddling with double-sums, when non-convergent-series are involved (as are the columnsums in the above matrix and the splitting in the numerical expression) must explicitely be justified as "legal"/algebraically consistent operation.
But because I encounter it not frequently, that such non-convergent double-sum schemes come out with the expected result without further ado, I think this is a specific nice observation here.

And the more algebraically manipulations come out to be consistent with the assumed value of a divergent series, the more is the hypothese acceptable, that this should be taken as the canonical numerical replacement for the series-expression ( like we do it with the rational fraction for the geometric series even in the divergent case (except for that with quotient $q=1$)) .

Answer 11

Euler's approach, but using algebra instead of subtraction of infinite series: Let $f(x)=(1-x)^{-2}$. Then $f(-x) = f(x) -4xf(x^2)$. Plug $x=1$ to get $f(-1)=-3f(1)$, whence $f(1)=-1/12$.

EDIT: This argument is a motivation for the mysterious value $-1/12$. Yes, $f(x) :=(1-x)^{-2}$ is undefined at $x=1$. If we define $f(1)=-1/12$, then the above identity holds for all $x$.

Answer 12

Suppose a rigorous way of doing a computation yields a well defined real number as the answer. But with shortcut formal manipulations that are not allowed (e.g. interchanging summations and integrations when that isn't allowed) one ends up with a divergent series and then the question is that given only the divergent series, can one guess what real number is most likely the answer to what the unknown original problem was.

This is similar to guessing that the next term of the integer sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 is probably 16 rather than e.g. 32431, even though the latter possibility cannot be ruled out. Strictly speaking this problem is not well defined, what one really is doing here is assuming that the sequence that is specified by the least amount of information is the most likely answer. The person who invented the puzzle had some simple algorithm in mind, therefore the much more complicated algorithm that would yield 32431 as the next number in the sequence is not the likely answer.

Similarly, the formal manipulations that yield the divergent series won't have introduced a lot of additional information, these are just generic mathematical manipulations that would have been correct when used in a wide class of problems, but not the one it actually has been applied to. This means that almost all the information about the unknown real number is present in the divergent series, it can be extracted from it by applying certain formal manipulations to the series that, like the unknown manipulations that led to the divergent series, are formally correct for a wide class of convergent series, but not in case of this divergent series.

Answer 13

As I recently showed in another answer, we have the wonderful pattern:

$$\sum_{k=1}^n1=n\implies\int_{-1}^0x~\mathrm dx=\zeta(0)\\\sum_{k=1}^nk=\frac{n(n+1)}2\implies\int_{-1}^0\frac{x(x+1)}2~\mathrm dx=\zeta(-1)\\\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}6\implies\int_{-1}^0\frac{x(x+1)(2x+1)}6~\mathrm dx=\zeta(-2)\\\sum_{k=1}^nk^3=\left[\frac{n(n+1)}2\right]^2\implies\int_{-1}^0\left[\frac{x(x+1)}2\right]^2~\mathrm dx=\zeta(-3)\\\vdots$$

This pattern works for all $\zeta(-k)$.

Answer 14

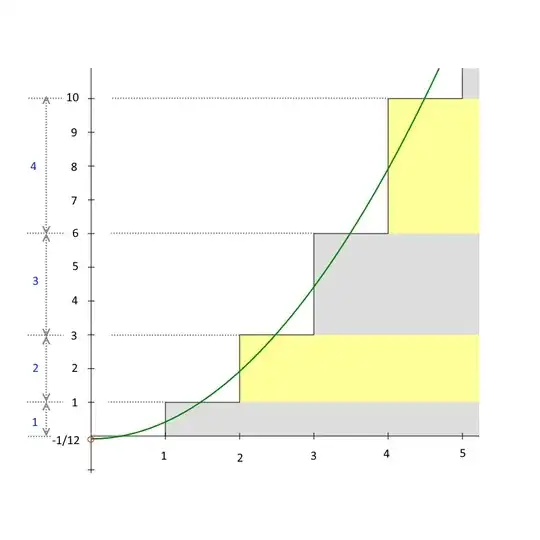
I like this simple graphical explanation.

There are first partial sums of the series 1 + 2 + 3 + 4 + ⋯ on picture. The parabola is their smoothed asymptote; its y-intercept is −1/12.

Answer 15

Here is a useful place for Euler's transform and the Dirichlet eta function:

$$\zeta(s)=\sum_{n=1}^\infty\frac1{n^s}$$

$$\eta(s)=\sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^s}$$

$$\zeta(s)-\eta(s)=\sum_{n=1}^\infty\frac{1+(-1)^n}{n^s}=\sum_{n=1}^\infty\frac2{(2n)^s}=2^{1-s}\sum_{n=1}^\infty\frac1{n^s}=2^{1-s}\zeta(s)$$

$$\zeta(s)-\eta(s)=2^{1-s}\zeta(s)\implies (1-2^{1-s})\zeta(s)=\eta(s)$$

$$\zeta(s)=\frac1{1-2^{1-s}}\sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^s}$$

After a quick application of Euler's transform, we get a nice analytic continuation to the entire complex plane.

$${\small E_1}\sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^s}=\sum_{n=0}^\infty\left[\frac1{2^{n+1}}\sum_{k=0}^n\binom nk\frac{(-1)^k}{(k+1)^s}\right]$$

Finally giving us

$$\zeta(s)=\frac1{1-2^{1-s}}\sum_{n=0}^\infty\left[\frac1{2^{n+1}}\sum_{k=0}^n\binom nk\frac{(-1)^k}{(k+1)^s}\right]$$

And at $s=-1$,

$$\zeta(-1)=-\frac1{12}$$

Answer 16

We must keep in mind here that the definition of addition of numbers does not yield a means to sum infinite series. So, one has to define what we mean by the sum of an infinite series. The conventional definition is that it is equal to the limit of the partial sums of the series. But taking this definition to be the universally correct definition is problematic, because when the limit of the partial sums does not exists, nothing is defined. In that case we say that the series diverges, but this is then a qualifier about the result of taking the limit of the partial sums having failed to yield a well defined value.

The correct interpretation should be that if a series diverges, that the limit of partial sums fails to provide for a definition of the sum of the series. Most people, however, will say that a diverging series means that the value of the series cannot be defined. This is then why this topic can sometimes be a bit controversial. There exist many methods to assign values to diverging series that will agree with the limit of partial series when applied to converging series.

Analytic continuation is one such method. Here one adds one or more parameters to the summand and consider the domain of those parameters where the series converges. One then analytically continues the result from that domain to the values of the parameters that specifies the original series. Very often this result is universal in the sense that a different way of introducing the parameters and a correspondingly different analytical continuation process would yield the same answer.

To see why the result of $-\frac{1}{12}$ is universal, I'll derive a summation formula that generalizes the ones given in Simply Beautiful Art's answer. For converging series, we have:

$$\sum_{k=1}^{\infty} f(k) = \int_{a}^{\infty}f(x) dx + \int_{a-1}^a S(x) dx \tag{1}$$

where $a$ is an arbitrary number that must be chosen such that the integral converges, and $S(x)$ is defined as follows. We first define $S(n)$ for integer $n$ as the partial sum of $f(k)$ from $1$ to $n$:

$$ S(n) = \sum_{k=1}^n f(k)$$

And we then analytically continue this to the complex plane by invoking Carlson's theorem. We can think of $S(x)$ for real $x$ as what you get by interpolating this using the values it attains at the integers. The conditions in Carlson’s theorem make $S(x)$ uniquely defined, e.g. the limit on the rate of growth in the imaginary direction takes away any freedom to add a function like $ \sin(\pi x)$ that vanishes on the set of integers to $S(x)$. We also need to invoke Carson’s theorem to define $f(x)$ when it’s originally only specified on the domain of integers.

The proof of (1) is very easy. One can start with assuming that $ S(x)$ is given. We then have that $f(x)= S(x) - S(x-1)$, and:

$$ \sum_{k=0}^{\infty} f(k) = \lim_{x\to \infty} S(x)$$

The first integral on the r.h.s. of (1) can be written as:

$$\begin{split}\int_a^{\infty}f(x) dx &= \lim_{R\to\infty} \left(\int_a^{R}S(x)dx - \int_{a-1}^{R-1}S(x) dx\right)\\ &= \lim_{R\to\infty} \int_{R-1}^R S(x) dx - \int_{a-1}^a S(x) dx\end{split}$$

The integral from $R-1$ to $R$ of $S(x)$ obviously tends to the same limit for $R$ to infinity as $S(x)$ for $x$ to infinity. The last term in (1) cancels out the integral from $a-1$ to $a$ in the above expression.

So, now we have proven (1) for converging series, what about diverging series? In that case we imagine that we could add parameters to the summand such that in a certain domain for those parameters the summation would be convergent and (1) would hold in the conventional sense. But without actually going about adding such parameters we can then see what must happen if we were to do so.

The integral from $a$ to infinity over $f(x)$ on the r.h.s. of (1) diverges, if we cut this off to $R$ then we’ll get diverging terms that are positive powers of $R$. If by adding parameters we would consider another domain where the summation would be convergent, these positive powers of $R$ must become negative powers of $R$ in that other domain, otherwise one cannot have a convergent series there.

If we then take the limit of $R$ to infinity there and then analytically continue that result back to the values of the parameters that yields the original summand here, then that amounts to analytically continue the constant term back here, which should simply yield the constant term we can evaluate directly here without going through this whole procedure of performing the analytic continuation.

Also the integral from $a-1$ to $a$ of $S(x)$ will have whatever value it evaluates to here. So, the conclusion is that the rule for computing the value of diverging series is to use (1) with the integral cut off to $R$ and then to discard all positive powers, logarithms etc, of $R$ and only keep the constant term of that integral.

In case of the sum of the natural numbers, we have to take $f(x) = x$. It’s then convenient to take $a = 0$. The integral from $0$ to $R$ is $\frac{R^2}{2}$ without any constant term and should therefore be discarded. Since $S(x) = \frac{1}{2} x (x+1)$ in this case, this means that the summation is given by:

$$ \int_{-1}^0 \frac{1}{2} x (x+1) dx = -\frac{1}{12}$$

So, we‘ve shown that the result is $-\frac{1}{12}$ by appealing to the existence of any arbitrary sort of analytical continuation without actually explicitly specifying one. It should therefore be clear that this result is not tied to the properties of the zeta function in a way that would make this result arbitrary.

Answer 17

Most of the answers here focus either on alternative methods for computing $\zeta(-1)$, or on why the statement "$\sum_{n=1}^{\infty} n = -1/12$" doesn't make sense. While these answers are good, I think that there is an underlying issue which is being missed out on. Specifically why is $\zeta(-1) = -1/12$ a reasonable answer to the question "What is $\sum_{n=1}^{\infty} 1/n$?" This answer is an attempt to fill this gap.

An Argument from Complex Analysis

In many areas of mathematics, it "makes sense" to take problems in the real numbers, extend them to the complex numbers, and solve the problem there. For example, the complex numbers are the algebraic completion of the reals, meaning that every polynomial with real (or even complex) coefficients has roots in the complex plane (this is the Fundamental Theorem of Algebra). In particular, every polynomial equation over the reals can be solved by complexifying the polynomial and looking for complex roots.^[1]

This strategy is often incredibly useful, as the complex numbers are very "rigid" in many important ways. In the complex numbers, "analytic"^[2] is synonymous with "smooth"^[3]—the same is not true in the real numbers, where a function can be smooth, but fail to be analytic (consider a smooth bump function, for example). In the current context, the most relevant result is the Identity Theorem, which says, roughly:

Theorem: Let $f$ and $g$ be two complex analytic functions defined on an (open, connected) domain $D$, and $S$ be a subset of $D$ which contains a limit point^[4]. If $f(s) = g(s)$ for all $s \in S$. Then $f(s) = g(s)$ for all $s \in D$.

In light of the Identity Theorem, the "game" is to extend an analytic function $f$ by finding an analytic function $g$ which agrees with $f$ on some set with a limit point, but which has a larger domain. The theorem implies that any such extension must be unique.

In the context of Riemann's zeta, we can start with the function $$\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}. $$ This series converges (and is analytic on) the set $\{s : \Re(s) > 1 \}$, which can be shown using some more general results on Dirichlet series. The trick, then, is to find a new function $\tilde{\zeta}$ which agrees with $\zeta$ on this half-plane, but which is analytic on a larger set. It has been a while since I have done this (I'm reviewing notes that I took in graduate school 8 years ago), but my recollection is that we can define a function $$ \xi(s) = \pi^{-s/2} \Gamma\left( \frac{s}{2} \right) \zeta(s) $$ on the half-plane $\{ s : \Re(s) > 1 \}$, demonstrate that this function is meromorphic on $\mathbb{C}$ and satisfies the functional equation $$ \xi(s) = \xi(1-s), $$ then define $$\tilde{\zeta}(s) = \pi^{s/2} \Gamma\left( \frac{s}{2} \right)^{-1} \xi(s). $$ There is a fair amount of work to be done here, and I am leaving out a ton of details, but the punchline is that $\tilde{\zeta}$ is entire (analytic on $\mathbb{C}$), and $$ \tilde{\zeta}(s) = \zeta(s)$$ for all $s$ with $\Re(s) > 1$. The Identity Theorem then guarantees that, for all intents and purposes, $\tilde{\zeta}$ and $\zeta$ are the same function, hence it is reasonable to drop the tilde at this point.

After all of this work, it has been shown that there is a function $\zeta$ which is analytic on $\mathbb{C}$, and the for any $s$ with $\Re(s) > 1$, the identity $$ \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} $$ holds. The argument concludes by showing that for this particular $\zeta$, it holds that $\zeta(-1) = -1/12$.

TL;DR: The function $s \mapsto \sum_{n=1}^{\infty} 1/n^s$ has a unique analytic extension to $\mathbb{C}$. When evaluated at $-1$, the value of this unique analytic extension is $-1/12$. If we start from Riemann's zeta function, and we care about the analaticity of that function on the right half-plane $\Re(s) > 1$, then there is no other possible way of assigning a value to the divergent series $\sum_{n=1}^{\infty} n$.

---

[1] Note: I am not claiming that polynomial equations have "nice" closed-form solutions in terms of radicals. I am asserting that if $p$ is a polynomial with real (or complex) coefficients, then there exists at least one complex number $s$ such that $p(s) = 0$. Actually finding such a root might end up being non-trivial.

[2] A function is analytic on some domain if it has a power series representation on that domain.

[3] A function is smooth if it has continuous derivatives of all orders.

[4] A limit point (or an accumulation point, or a cluster point) of a set $S$ is a point $s \in S$ such that if $U$ is any neighborhood of $s$, there exists some point $t \in S \cap U$. That is, there are points of $S$ which are "arbitrarily close" to $s$.

Answer 18

Today I stumbled on a totally elementary derivation of this that does not rely on regulators or any reference to the Riemann Zeta Function. We start by looking at the geometric series

$$ \frac{1}{1-x} = 1 + x + x^2 + x^3 + x^4 + ... $$

Now instead of computing the taylor series of this function we can to compute its $\log$-taylor series that is the coefficients in terms of $\log(x)^n $

First we recall that $x^n = e^{n \log(x)} $ then it follows that:

$$ \frac{1}{1-x} = 1 + e^{2 \log(x)} + e^{3 \log(x)} +e^{4 \log(x)} + ... $$

Therefore:

$$ \frac{1}{1-x} = 1 + \left(1 + 2 \log(x) + \frac{1}{2!} \left( 2 \log(x) \right)^2+ ... \right) + \left( 1 + 3 \log(x) + \frac{1}{3!} (3 \log(x))^2 \right) + ... $$

Which we can re-arrange as:

$$ \frac{1}{1-x} = 1 + \left(1+1+1... \right) + (1+2+3+4....) \log(x) + \frac{1}{2!} (1^2+2^2 +3^2 ...) \log(x)^2 +... $$

Which obviously don't converge.

But we have ONE more observation. We can get the log taylor series one other way. First we find the laurent series (since theres a negative power term) of

$$ \frac{1}{1-e^x} = -\frac{1}{x} - \frac{1}{2} - \frac{1}{12}x + \frac{1}{720}x^3 + ... $$

So we conclude then that

$$ \frac{1}{1-x} = -\frac{1}{\ln(x)} + \frac{1}{2} - \frac{1}{12}\ln(x) + \frac{1}{720}\ln(x)^3 + ... $$

So then in order for this to be consistent with our earlier result it must be the case that

$$ 1 + \left( 1 + 1 + 1 ... \right) = 0! *\left( \frac{1}{2} \right) \rightarrow \left( 1 + 1 + 1 ... \right) = -\frac{1}{2} $$

$$ 1 + 2 + 3 + 4 ... = (1!) *\left( - \frac{1}{12} \right) = - \frac{1}{12} $$

$$ 1^2 + 2^2 + 3^2 + 4^2 ... = 2! * 0 = 0 $$

$$ 1^3 + 2^3 +3^3 + 4^3 ... = 3!* \frac{1}{720} = \frac{1}{120} $$

etc..

CAVEAT:

There is that mysterious $- \frac{1}{\ln(x)}$ that is not accounted for. I'm not really sure what to do about that, although I have some undeveloped ideas brewing which ill update this with once i have refined them.

Another Elementary Approach:

A function $G(x)$ can be written as a series of the form $a_n f(x)^n$ for your choice of $f(x)$ if we define the operator $ D = \frac{1}{f'(x)} \frac{d}{dx}$ and $c$ is a constant such that $\frac{1}{f'(c)}$ is well defined and $f(c)=a$ then

$$ G(x) = G(c) + D[f](c)(f(x)-a) + \frac{1}{2!}D^2[f](c)(f(x)-a)^2 + \frac{1}{3!}D^3[f](c)(f(x)-a)^3 ... $$

Now if $G(x)$ has a singularity $x=c$ as is the case for $G(x)=\frac{1}{1-x}$ $f(x) = \ln(x)$, $c=1$, then you basically need an analogue of the residue theorem to extract its laurent series w.r.t $f$, i'm working on building that right now, but assuming such a thing can be constructed it gives us a different elementary framework which explains the $-\frac{1}{\ln(x)}$ term, but the mystery of why the first method doesn't catch it remains...