-2

I'm learning special functions by programming them, largely for fun. This post discussed why or how $\zeta(-1)=-1/12$, while my interest is how to numerically evaluate the zeta function at -1 and other points on $\mathbb{R}$.

Corresponding to the definition of Riemann zeta function $$ \zeta(z)= \sum_{n=1}^\infty n^{-z} $$ where $n^{a+bi}=n^a[\cos(b \ln n)+i\sin (b \ln n)]$, my codes read:

public static double[] R_powerZ(double n, double[] v){
    double a=v[0];
    double b=v[1];
    double theta= b* Math.log(n);
    double[] c={ Math.cos(theta), Math.sin(theta)};
    return M.scale(c,  Math.pow(n, a));
}

public static double[] zeta(double[] tau, int interation) {
    double[] re = new double[2];
    for (int i = 1; i <= interation; i++) {
        double[] v = R_powerZ(i, M.scale( tau ,-1));
        M._add(re, v);
    }
    return re;
}

Let $z=-1$ and $n=50$, the numerical result is (1275,0). I can see that the value will increase when n increases, does it means that the series is divergent when $z=-1$?. I also tried $\zeta(-0.99999)=(1274.9563...,0)$ which indicates that the function is continuous around -1.

Such numerical evaluation is far from the result of $\zeta(-1)=1+2+3+\cdots=-1/12$. Further, it's crazy to get a negative value from this summation!

I read this old post. Partially convinced by the proof there, my question is: is there a constructive way (by programming, by literal summation as the definition the zeta function) to calculate the value of $\zeta(z)$? If not, why we need a definition of $\sum_{n=1}^\infty n^{-z}$ at all?

Put it differently, how to get a good approximation of the zeta function by programming from scratch? This post did not explain any experiments (e.g. physical experiments or numeric algorithms) from which the value of the zeta function can be measured.

A convenient formula from wiki page is using Bernoulli number $$ \zeta(2n)= \frac{(-1)^{n+1} B_{2n}(2\pi)^{2n}}{2 (2n)!} $$ for positive even integer, and for nonpositive integer $$ \zeta(-n)= (-1)^n\frac{B_{n+1}}{n+1} $$ both give the "right" results of $\zeta(0)$ and $\zeta(-1)$. But how can the two formula comply with the original definition $\sum_{n=1}^\infty n^{-z}$?

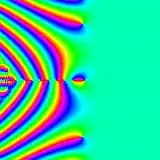
Then I tried a 'globally' convergent series $$ \zeta(z)=\frac{1}{1-2^{1-s}} \sum_{n=0}^\infty \frac{1}{2^{n+1}} \sum_{k=0}^n \binom{n}{k} \frac{-1^k}{(k+1)^s} $$ from the wiki page, the corresponding codes yield this image (the color denotes the argument) enter image description here

Hopefully I am on the right direction.

whitegreen
  • 1,583
  • 5
    The reimann zeta function is defined by a series when $re(z) > 1$. Anywhere else, the function is defined by an analytic continuation. Frankly, you've fallen for a pop math result that isn't typically well explained. – Kaynex Oct 31 '17 at 03:36
  • 1
    Possible duplicate of Why does $1+2+3+\cdots = -\frac{1}{12}$? – anomaly Oct 31 '17 at 03:49
  • 2
    Consider the function $f(x)=1+x+x^2+\cdots$. If I tell you $f(3)=-1/2$, you'll object that your computer shows the series diverges, and anyway you can't add positive numbers and get a negative answer. But $f(x)$ has another formula, $f(x)=1/(1-x)$, and using that alternative formula, $f(3)=-1/2$. It's the same for the zeta function, only the "alternative formula" is more complicated than it is in my example. – Gerry Myerson Oct 31 '17 at 03:50
  • @anom, note that OP is well aware of that earlier question, and finds it unsatisfactory. – Gerry Myerson Oct 31 '17 at 03:51
  • @GerryMyerson: Right, but I think everything we've had to say about $\zeta(-1)$ is in that post or linked to or from it. (And, frankly, any idea about a physical experiment is probably out of scope for this board anyway.) – anomaly Oct 31 '17 at 03:52
  • @GerryMyerson but the series only converges i.e $\sum x^k = \frac{1}{1-x}$ makes sense only when $|x|<1$ – AlvinL Oct 31 '17 at 05:31
  • @Alvin, that's the point – that's what makes it like the zeta function, where the definition as a sum makes sense only for real part of $z$ exceeding 1. – Gerry Myerson Oct 31 '17 at 09:34
  • @GerryMyerson "OP is well aware of that earlier question" Rather, it seems OP didn't do their homework since, if they had simply read that earlier question and its comments, they would not even try to evaluate $\zeta(-1)$ by considering partial sums $\sum\limits_{k=1}^nk$. – Did Oct 31 '17 at 10:17
  • @Did, I have no doubt that an understanding of what's at the earlier question would help OP, but it seems OP can't get there without some external aid. – Gerry Myerson Oct 31 '17 at 11:05
  • "the color denotes the argument" The argument of $\zeta(z)$ is $z$. What did you really mean? – Gerry Myerson Oct 31 '17 at 11:10
  • @GerryMyerson But then why do they stick to the absurd statement we know all too well because we meet it too often, although said statement is properly debunked on the other page? "Understanding" is not the problem here, it seems... – Did Oct 31 '17 at 12:12
  • The very first equality in the title is simply wrong. $\zeta(-1)$ is not defined as $1+2+3+\ldots$, also because $1+2+3+\ldots$ is diverging. – Jack D'Aurizio Oct 31 '17 at 15:37
  • @Jack et al., I'm not upset to see this question closed, but the boilerplate, "Please improve the question by providing additional context, which ideally includes your thoughts on the problem and any attempts you have made to solve it," seems particularly inappropriate here, and of no help to OP. – Gerry Myerson Oct 31 '17 at 23:25

1 Answers1

3

Numerical evaluation of special functions is a big subject — simply plugging in numbers into the simplest things often gives poor results.

Trying to estimate $\zeta(-1)$ by the partial sums of this series should be expected to give especially poor results — the limit of its partial sums only exists when $\mathrm{Re}(z) > 1$, and $z= -1$ does not have that property.

Similarly, estimating $-1/12$ by the partial sums of the series $1 + 2 + 3 + \ldots$ is also doomed to failure; the summation used here is not "limit of partial sums", it is "zeta regularization", so you should not expect partial sums to have anything to do with the value of the sum.

Wikipedia gives a great many formulas and identities that $\zeta(z)$ satisfies. All of the infinite sums on the wikipedia page, I believe, are the ordinary "limit of partial sums" meaning, so you can use partial sums to estimate the value.