3

We all know that $\dfrac{f(x)}{f(x)} = 1$ (where $f(x) \neq 0$) and that $\sum_{n=1}^{x} n = \dfrac{x(x+1)}{2}$.

So, given $f(x) \stackrel{\text{def}}{=} \sum_{n=1}^{x} n$, we show that $\dfrac{f(x)}{f(x)} = \dfrac{\frac{x(x+1)}{2}}{\frac{x(x+1)}{2}} = \dfrac{x(x+1)}{x(x+1)} = 1$ (where $x \not\in \{-1, 0\}$).

From this, it seems logical that $\dfrac{f(\infty)}{f(\infty)}$ would equal $1$. Now, before you bash me for using $\infty$ like a number, I know $\infty$ isn't a number and can't be used as one, but bear with me. However, WolframAlpha begs to differ and spits out $(indeterminate)$. I assume it's calculating $\dfrac{\frac{\infty(\infty+1)}{2}}{\frac{\infty(\infty+1)}{2}} = \dfrac{\infty(\infty+1)}{\infty(\infty+1)} = \dfrac{\infty}{\infty}$ which is $(indeterminate)$.

All that makes sense, but because $\infty$ isn't a number, you can't calculate $f(\infty)$ and (from what I've been taught) instead must calculate $\lim_{x \to \infty} \dfrac{f(x)}{f(x)}$, which works out as long as $x \not\in \{-1, 0\}$:

$\dfrac{f(1)}{f(1)} = \dfrac{1}{1} = 1$

$\dfrac{f(2)}{f(2)} = \dfrac{3}{3} = 1$

${}\qquad\vdots$

$\dfrac{f(10^{10})}{f(10^{10})} = \dfrac{50\space000\space000\space005\space000\space000\space000}{50\space000\space000\space005\space000\space000\space000} = 1$

And, of course, it works out to be $1$ as long as $x \not\in \{-1, 0\}$. In addition, when graphed as $\dfrac{\frac{x(x+1)}{2}}{\frac{x(x+1)}{2}}$ (WolframAlpha doesn't like the sum form), you get none other than a $y = 1$ plot (with holes at $x \in \{-1, 0\}$):

plot

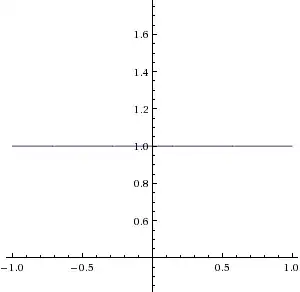
What gives? Is WolframAlpha wrong again, or have I just been taught incorrectly again (like how $\sqrt{x^2} = x$)?

If I wanted to use the analytically continued Riemann-Zeta function, I could use $\zeta(-1)$ instead of $f(\infty)$, I get $\dfrac{\zeta(-1)}{\zeta(-1)} = \dfrac{-\frac{1}{12}}{-\frac{1}{12}} = 1$. But this is out of the scope of the question.

Community
  • 1
Cole Tobin
  • 1,399
  • 4
  • 14
  • 23
  • This is conceptually similar to this one http://math.stackexchange.com/questions/80262/why-is-int-infty-infty-fracxx21-dx-not-zero – leonbloy Jun 16 '14 at 01:42

3 Answers3

9

Sure,

$$\lim_{x\to\infty}\frac{\displaystyle\sum_{n=1}^xn}{\displaystyle\sum_{n=1}^xn}=1.$$

However, $\displaystyle\sum_{n=1}^\infty n$ is defined to be $\displaystyle\lim_{x\to\infty}\sum_{n=1}^x n$, which does not exist, hence

$$\frac{\displaystyle \sum_{n=1}^\infty n}{\displaystyle \sum_{n=1}^\infty n} =\frac{\displaystyle \lim_{x\to\infty}\sum_{n=1}^x n}{\displaystyle \lim_{x\to\infty}\sum_{n=1}^x n}$$

is a ratio of two things that do not exist. So, of course, the ratio does not exist.

There are strict rules that tell us when it is okay to pull $\lim$s out of expressions, or to consolidate multiple $\lim$s together, and you have been ignoring these rules.

anon
  • 151,657
1

$+\infty$ is a number, can be used as a number (although the extended real numbers don't satisfy all of the algebraic identities that the real numbers do), and $(+\infty)/(+\infty)$ is undefined (in the same way that $0/0$ is undefined).

And $\sum_{n=1}^{\inf} n = +\infty$.

The expression $\frac{\sum_{n=1}^{\inf} n}{\sum_{n=1}^{\inf} n}$ is not indeterminate: it is undefined.

0

The numerator and denominator are $\infty$, so you're asking wolfram alpha "What is $\infty/\infty?$" which doesn't have an answer. If instead you asked the different question: What is $\lim_{N\rightarrow\infty} \sum_0^Nn / \sum_0^Nn$? you would get 1.

mathematician
  • 2,450