10

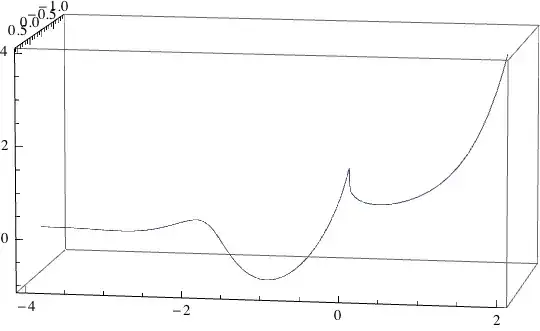
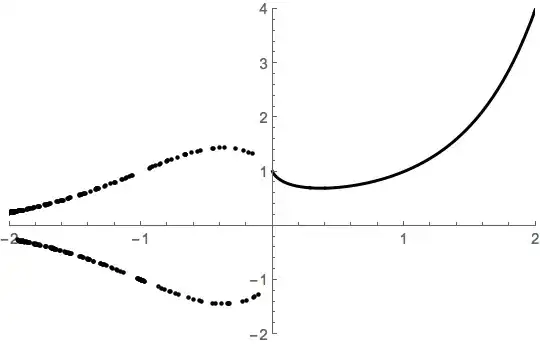
The function $f(x) = x^x$ gives a complex number only if x has an even denominator. I'm not sure about irrational numbers. Why, then, is the best graph I can find of that function that of Wolfram Alpha, which plots adjacent sinusoidal waves for the real and imaginary parts, even at well-defined values such as $x = -\frac{1}{3}$? (And that's the plot that includes imaginary numbers; the real-valued plot shows nothing below zero.) I suspect this might be because the results are computed in a way that requires imaginary numbers.

The number of values for which the function is defined is infinite, but the values for which it is not are also infinite. So how should the graph look below zero?

(Note that in order to avoid another point where the function may be undefined I'm assuming that $0^0 = 1$.)

Lee Sleek
  • 1,682
  • Is the plot returning the princpal root instead of the real valued root? http://www.wolframalpha.com/input/?i=%28-1%2F3%29%5E%28-1%2F3%29 – MattyZ May 17 '13 at 02:31
  • Try putting both roots into WA yourself and see what happens. – Lee Sleek May 17 '13 at 02:35

1 Answers1

14

Although it doesn't deal directly with $x^x$, here's a WolframAlpha blog post that details how real and complex roots are currently treated by WolframAlpha.

As far as $x^x$ goes, the plot does indeed show the real and imaginary parts of the principal value of $x^x$ on the same axis. Another approach is to plot the complex point itself in a plane that's perpendicular to the $x$-axis at the corresponding point. This leads to a spectacular image called the $x^x$-spindle, which was described in a great paper in Mathematics Magazine back in 1996. This looks like so:

enter image description here

Using the fact that the complex logaritm is multi-valued, this can be generalized to obtain more threads on the spindle:

enter image description here

It sounds like you've seen the claim that $(p/q)^{p/q}$ is defined for $p$ negative and $q$ odd and positive. Thus the graph might look something like so.

enter image description here

From the complex perspective, the dots arise as spots where one of the spiral threads punctures the $x$-$z$ plane.

Note that the Mathematica code for these images is all provided in this answer over on mathematica.SE.

Community
  • 1
Mark McClure
  • 30,510
  • What is the minimum value in image #1? Also, $(-1)^{-1}$ is $-1$ and not $1$. – Lee Sleek May 17 '13 at 18:41
  • @LeeSleek I don't understand the question. – Mark McClure May 17 '13 at 18:45
  • In the first image, the graph experiences a dip after it passes the y-axis, and then rises again. What value of x produces the smallest value there? – Lee Sleek May 17 '13 at 18:58
  • Thanks for the answer as well. – Lee Sleek May 17 '13 at 19:06
  • I also notice that in image number two, at the place where the graph reaches its minimum the the threads of the spindle disappear. Again, why is that? – Lee Sleek May 18 '13 at 01:22
  • 1
    @Lee Sleek: You can find the minimum of $x^x$ for $x > 0$ by calculus, using a method often called logarithmic differentiation. Let $y = x^{x}.$ Taking the logarithm of both sides gives $\ln y = \ln\left(x^x\right) = x\ln x.$ Now find $y'$ by implicit differentiation. You'll get $y' = x^x \left(\ln x + 1 \right).$ Setting this equal to $0$ and solving for $x$ gives $x = e^{-1} = 0.367879 \dots$ See also this WolframAlpha webpage and these related examples. – Dave L. Renfro May 20 '13 at 20:20
  • I was referring to the dip within the negative numbers. – Lee Sleek May 20 '13 at 21:44
  • @LeeSleek Based on the real plane, the minimum of $x^{x}$ in the negative domain must have rational x-value that has an odd integer as a numerator and an odd integer as a denominator(odd/odd). Otherwise, the minimum fails to exist. Now if you know that $x^x$ is equal to $(-x)^{x}$ for (-odd/odd) values you will find that the minimum is at $x=-\frac{1}{e}$. Since the x-value is already irrational, there is no minimum. – Arbuja Dec 09 '15 at 20:59
  • 1
    thank you, that explanation is phenomenal. I'm fascinated. It's crazy I did so much math and never really looked at x power x – v.oddou May 26 '20 at 15:51
  • 2
    @v.oddou Thanks, I'm glad you like it! Here's an interactive 3D version of the spindle: https://observablehq.com/@mcmcclur/the-xxx-xxx-spindle – Mark McClure May 26 '20 at 15:59
  • It would be interesting to see the plot of the bottom graph for the real and imaginary part both on the $x,y$ plane using this convention – Тyma Gaidash Jan 14 '24 at 16:12