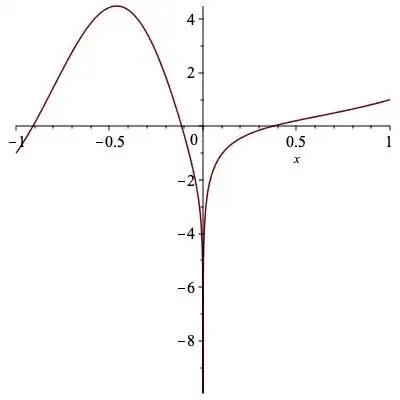
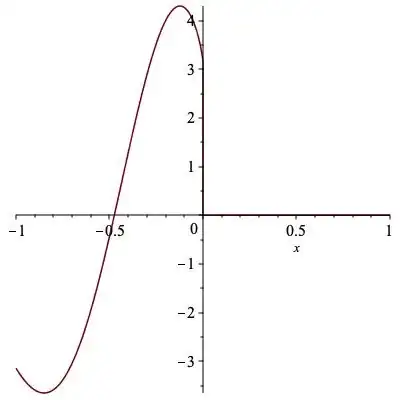
The function $f(x)=x^x$ is only defined for negative values of $x$ if $x$ is a rational number $a/b$, where $b$ is odd. Initially, I thought this meant that the limit $$ f'(a)=\lim_{h\to0}\frac{(a+h)^{a+h}-a^a}{h} $$ cannot exist if $a$ is a negative number, since every neighbourhood of $a$ would contain values for which $x^x$ does not make any sense at all. However, this post—about $\lim_{x\to0}\frac{\sin(1/x)}{\sin(1/x)}$—suggests that provided every neighbourhood of $a$ contains values for which $x^x$ is defined, there is no issue with taking limits at the point.
So if $a$ is negative number that is in the domain of $f$, then does $f'(a)$ exist? And if so, is there a general formula for $f'(a)$?