4

I have a question about the graph of $f(x) = x^x$. How come the graph doesn't extend into the negative domain? Because, it is not as if the graph is undefined when $x=-5$. But according to the graph, that seems to be the case. Can someone please explain this?

Thanks

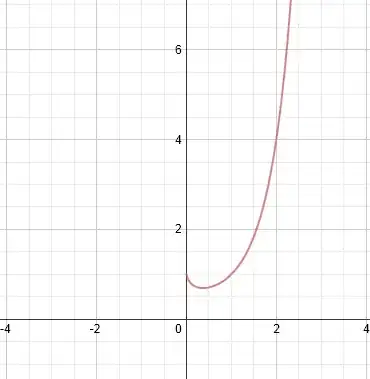
enter image description here

Jeel Shah
  • 9,306
  • Very related post – amWhy May 21 '13 at 15:26
  • @amWhy I was actually inspired by that post but I didn't think they were related for some reason. Maybe both posts can complement each other? – Jeel Shah May 21 '13 at 15:27
  • 2
    Negative numbers cannot be raised to arbitrary real powers and produce real outputs. Just consider what $(-1/2)^{-1/2}$ would be. However you can extend this function in a "nice" way by looking at $|x|^x$. – 2'5 9'2 May 21 '13 at 15:28
  • @alex.jordan I put $(-1/2)^{-1/2}$ and I get imaginary but when I put $(-5)^{-5}$ I get answer that is $-0.00032$. Can you provide more detail please? – Jeel Shah May 21 '13 at 15:50
  • 3
    @gekkostate Raising a negative number to a whole number is not a problem. $(-5)^{-5}$ means $1/((-5)(-5)(-5)(-5)(-5))$. But $x^{-1/2}$ should be a square root of $x$,and if $x$ is negative, no square roots are real. And then there are things like $(-2)^{\pi}$. What would that possibly mean to you? At least with $2^{\pi}$ we could approximate $\pi$ with a rational number $m/n$ and $2^{\pi}$ would be something close to $\sqrt[n]{2^m}$. But for negative bases we'll have trouble executing that $\sqrt[n]{}$. – 2'5 9'2 May 21 '13 at 15:56
  • Graphing Calculators have trouble graphing points. (So it is defined for $x=-5$: $(-5)^{-5}=\displaystyle\frac{1}{(-5)^5}=-\frac{1}{3125}= -0.00032$. On my Graphing Calculator, a TI89 Titanium, the points do not show, but if I plug in the value $x=-5$, I get $-0.00032$ – Justin May 21 '13 at 20:04
  • This looks like a duplicate of this question – robjohn May 22 '13 at 14:40
  • 1
    @JeelShah Hopefully my answer down below is the one you were looking for. – Arbuja Dec 10 '15 at 01:02
  • @alex.jordan Remember the crucial property that if $x_1=x_2$ then $f(x_1)=f(x_2)$ for $x^x$. Also remember that $e^{x\ln{x}}=x^x$ when $x<0$. – Arbuja Dec 13 '15 at 02:18

2 Answers2

1

A more direct answer is the reason your graphing calculator doesn't graph when $x<0$ is because there are infinite undefined "holes" and infinite defined points in the real plane. Even when you restrict the domain to $[-2,-1]$ this will still be the case.

Note that for $x^x$ when $x<0$ if you calculate for the output of certain x-values (using the Texas I-85) you will have...

$$x^x=\begin{cases} (-x)^x & x=\left\{ {2n\over 2m+1}\ |\ n, m \in \Bbb Z\right\}\frac{\text{even integer}}{\text{odd integer}}\\ -(-x)^{x} & x=\left\{ {2n+1\over 2m+1}\ |\ n, m \in \Bbb Z\right\}\frac{\text{odd integer}}{\text{odd integer}}\ \\ \text{undefined} & x=\left\{ {2n+1\over 2m}\ |\ n, m \in \Bbb Z\right\}\bigcup \left\{\mathbb{R}\setminus{\mathbb{Q}}\right\} \left(\frac{\text{odd integer}}{\text{even integer}},\text{irrational numbers}\right) \end{cases}$$

(Just remember to simplify fractions all the way until the denominator is a prime number (ex: $2/6\to1/3$))

This is because when we have $x^a$ it can only extend to the negative domain if $a$'s denominator is odd (ex: $x^{1/3},x^{2/3}$).

Thus there are infinite undefined values from $[-2,-1]$ that are still (even/odd) when simplified. For example $( -3/2,-1/2)$ are undefined but so is $ (-19/10, -17/10, -15/10...-11/10)$ and $(-199/100, -197/100, -195/100,.....-101/100)$. This includes irrational numbers.

There is also infinite defined values. There are infinite defined values that have positive output and infinite defined values that have a negative output. For example there is $(-2,-4/3$), ($-2,-24/13,-22/13,-16/13...-14/13)$ and $(-2,-52/27,-50/27,-48/27,-46/27,-44/27...-28/27)$ that are still positive.

Then there is $(-5/3,-3/3)$, $(-25/13,-23/13,-21/13,-19/13..-13/13)$ and $(-53/27,-51/27,-49/27,-47/27,-45/27,-43/27...-27/27)$ that is negative.

Because the function is so "disconnected" with undefined holes and real numbers the graphing calculator still fails to register a graph of $x^x$ when $x<0$.

Thus when you see $x^x$ with the three graphs in the peicewise definition note that I am hiding the infinite holes that exist for ${x}^{x}$.

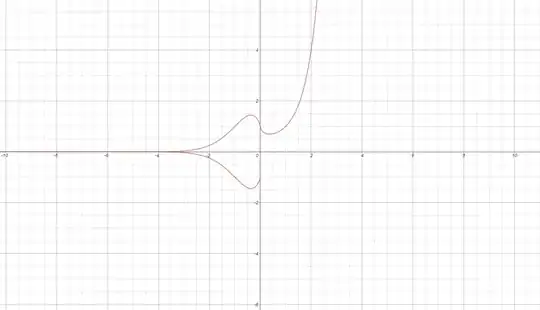
Now since the outputs for the negative domain can be positive or negative we have two "trajectories". Thus we must graph $\left(-x\right)^{x}$ and $-\left(-x\right)^{x}$ with $x^x$. x^x: The complete graph

However, if you want to graph $x^x$ to seem "more continuous" you can either $|x|^{x}$ or $\text{sgn}{\left(x\right)}|x|^{x}$.

Arbuja
  • 1
1

Well, for a START, what would happen if your exponents were to be -0.5, -1.5, -2.5, -3.5 etc? Convert that into radical notation and try to evaluate for those negative x-values. (And there is lots more going on for negative x-values)

imranfat
  • 10,029