Graph of $y=x^x$ for $x<0$

Question

I have been wondering about the graph of $y=x^x$. Most graphing calculators will quite happily graph it up to $0$, but after that they don't do anything else. Basic calculation suggests that, while for some points ($x=-\frac 12$) there are no real number solutions, for others ($x=-1,-2,-3$ etc.) there are solutions. Why, if at all, do the graphing calculators stop at $0$, and can anyone produce a graph of the real number solutions of $y=x^x$ past the $0$ point? Thanks.

possible duplicate of Can the graph of $x^x$ have a real-valued plot below zero? — apnorton, Jan 22 '14 at 15:28
The function is somewhat pathological for negative values. Calculators stay away from that. Anyway, $|x|^x$ will work. — , Dec 09 '15 at 20:53
$|x|^x$ equals $(x^2)^{x/2}$, if you don't like the absolute value sign. — Akiva Weinberger, Dec 09 '15 at 23:26
@AkivaWeinberger There is two "trajectories" when $x<0$ not one. You can check my answer below. — Arbuja, Dec 10 '15 at 00:28
@Arbuja: taking $+$ makes it a continuous function; $-$ is somewhat artificial; you can't take both signs at the same time. — , Dec 10 '15 at 07:36
@YvesDaoust The function has points that ossilate between the +/- when $x<0$ depending on, for $p/q$ where q is odd, if p is even or odd. Ignoring the fact that some negative values have a negative output can mislead people that there are no negative values when $x<0$. — Arbuja, Dec 10 '15 at 13:05
@Arbuja: oubviously I never claimed that $x^x$ and $|x|^x$ are the same thing. I said that a calculator will make more sense of $|x|^x$. — , Dec 10 '15 at 13:18

J.R. · Accepted Answer · 2015-12-10T16:52:27.553

Note that $f(x)=x^x = e^{x\ln(x)}.$ Since $e^x>0$ for $x\in\mathbb{R}$, there exists no real logarithm of negative real numbers.

However, by the Euler identity $e^{\pi i}=-1$, therefore you could say that "$\ln(-1)=\pi i$", which is a complex number. The problem with that is that the exponential function is periodic, i.e. $e^{(2k+1)\pi i}=-1$ for every odd number $2k+1$, $k\in\mathbb{Z}$. Therefore you could just as well say that "$\ln(-1)=3\pi i, -\pi i, \dots$". See multivalued function, complex logarithm.

The graph which you see in Wolfram Alpha gives you for negative real values the real and imaginary part corresponding to using the principal branch (one choice of values for the logarithm which is somehow canonical) of the logarithm.

You might want to check my answer. – Arbuja Dec 09 '15 at 20:47 — Arbuja, Dec 09 '15 at 20:47
Just remember that $e^{x\ln{x}}\neq{x}^x$ when $x<0$. – Arbuja Dec 13 '15 at 14:00 — Arbuja, Dec 13 '15 at 14:00

score 1 · Answer 2 · edited Aug 08 '17 at 17:58

A more direct answer is the reason your graphing calculator doesn't graph when $x<0$ is because there are infinite undefined "holes" and infinite defined points in the real plane. Even when you restrict the domain to $[-2,-1]$ this will still be the case.

Note that for $x^x$ when $x<0$ if you calculate for the output of certain x-values (using the Texas I-85) you will have...

$$x^x=\begin{cases} (-x)^x & x=\left\{ {2n\over 2m+1}\ |\ n, m \in \Bbb Z\right\}\frac{\text{even integer}}{\text{odd integer}}\\ -(-x)^{x} & x=\left\{ {2n+1\over 2m+1}\ |\ n, m \in \Bbb Z\right\}\frac{\text{odd integer}}{\text{odd integer}}\ \\ \text{undefined} & x=\left\{ {2n+1\over 2m}\ |\ n, m \in \Bbb Z\right\}\bigcup \left\{\mathbb{R}\setminus{\mathbb{Q}}\right\} \left(\frac{\text{odd integer}}{\text{even integer}},\text{irrational numbers}\right) \end{cases}$$

(Just remember to simplify fractions all the way until the denominator is a prime number (ex: $2/6\to1/3$))

This is because when we have $x^a$ it can only extend to the negative domain if $a$'s denominator is odd (ex: $x^{1/3},x^{2/3}$).

Thus there are infinite undefined values from $[-2,-1]$ that are still (even/odd) when simplified. For example $(-3/2,-1/2)$ are undefined but so is $ (-19/10, -17/10, -15/10...-11/10)$ and $(-199/100, -197/100, -195/100,.....-101/100)$. This includes irrational numbers.

There is also infinite defined values. There are infinite defined values that have positive output and infinite defined values that have a negative output. For example there is $(-2,-4/3$), ($-2,-24/13,-22/13,-16/13...-14/13)$ and $(-2,-52/27,-50/27,-48/27,-46/27,-44/27...-28/27)$ that are still positive.

Then there is $(-5/3,-3/3)$, $(-25/13,-23/13,-21/13,-19/13..-13/13)$ and $(-53/27,-51/27,-49/27,-47/27,-45/27,-43/27...-27/27)$ that is negative.

Because the function is so "disconnected" with undefined holes and real numbers the graphing calculator still fails to register a graph of $x^x$ when $x<0$.

Thus when you see $x^x$ with the three graphs in the piecewise definition note that I am hiding the infinite holes that exist for ${x}^{x}$.

Now since the outputs for the negative domain can be positive or negative we have two "trajectories". Thus we must graph $\left(-x\right)^{x}$ and $-\left(-x\right)^{x}$ with $x^x$.

However, if you want to graph $x^x$ to seem "more continuous" you can either $|x|^{x}$ or $\text{sgn}{\left(x\right)}|x|^{x}$.

Your evaluations (like many who write about this, both online and in print) make use of a procedure that assumes when one inputs a rational number, you reduce it to lowest terms and then interpret the exponentiation as a power-root combination. That's fine if these are given in advance as part of the instructions for calculating the values, but they weren't, and so here's a problem. A crucial property of a function is that if $x_1=x_2,$ then $f(x_1)=f(x_2).$ However, this fails with what you're doing when $x_1=\frac{1}{3}$ and $x_2=\frac{2}{6}.$ — Dave L. Renfro, Dec 09 '15 at 21:08
My point is that simply writing $y=x^x$ doesn't say anything about whether rational values of $x$ are to be reduced or not, so the entire issue of what $x^x$ (as a real valued function of a real variable) means for negative values of $x$ is an ill posed question. That's why college algebra and precalculus texts all assume $b>0$ when discussing the exponential function $b^x.$ — Dave L. Renfro, Dec 09 '15 at 21:45
I guess you could start by saying something like this: In the context of a real-valued function of a real variable, the expression $x^x$ is problematic for $x<0,$ since the value of $x^x$ appears to depend on how you express $x$ (appears to be defined if $x$ is $-\frac{1}{3}$ but not if $x$ is $-\frac{2}{6}).$ However, making the assumption that many people do, namely that in evaluation $x^x$ for negative rational values of $x$ we express $x$ as a reduced quotient of integers and perform the corresponding power and root operations, we are led to $\ldots$ — Dave L. Renfro, Dec 09 '15 at 22:15
Incidentally, a related discussion is at What is the domain of $x^x$. And note that both there and in my first comment here, I intended $x_1$ and $x_2$ to be $-\frac{1}{3}$ and $-\frac{2}{6}.$ — Dave L. Renfro, Dec 09 '15 at 22:21
See my comments about this answer versus mine in the thread after my answer. If you are going to take this approach, you should probably add a line to your function definition that declares $x^x$ to be undefined when $x$ is negative nonrational too. — 2'5 9'2, Dec 10 '15 at 21:23
@enthdegree I explored with the calculator and then checked it by using mathematics.Then I inferred from there. — Arbuja, Dec 11 '15 at 17:02

score 0 · Answer 3 · answered Dec 10 '15 at 20:13

0

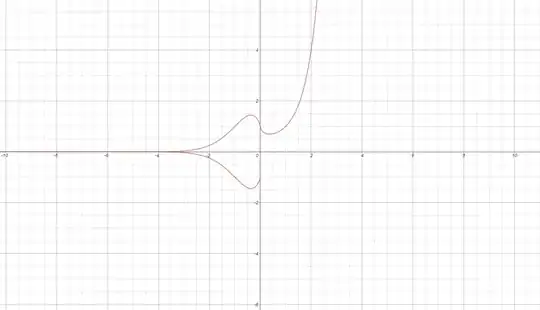
Graph $y=\left\lvert x\right\rvert^x$ instead.

You can't raise negative real numbers to arbitrary powers and expect to get a real output. For instance $(-1/2)^{-1/2}$ is not real; although there are two nonreal complex numbers this could be interpreted to mean. Expressions like $(-\pi)^{-\pi}$ are even more problematic.

But $y=\left\lvert x\right\rvert^x$ gives an interesting, smooth curve (with a vertical tangent at $(0,1)$.)

answered Dec 10 '15 at 20:13

2'5 9'2

54,717

Still you should not ignore the $-|x|^x$ when $x<0$. – Arbuja Dec 10 '15 at 20:19
Plus you need to explain why the graph does not register in graphing calculators. – Arbuja Dec 10 '15 at 20:19
@Arbuja I don't really understand your first comment. As for the second, I have addressed that when I explain how $(\text{negative real})^{\text{non-integer}}$ does not provide a real number result. Hence, a graphing calculator has nothing to plot. – 2'5 9'2 Dec 10 '15 at 21:07
1

@Arbuja In your answer, you use a definition of raising to negative powers that is not what mathematicians use. It appears that you believe $(-8)^{-1/3}=\frac{1}{\sqrt[3]{-8}}=\frac{1}{-2}$. This may shock you, but $(-8)^{-1/3}\neq\frac{1}{\sqrt[3]{-8}}$. The left side means $\exp(-\ln(-8)/3)$, where "$\ln(-8)$" can be any complex number that exponentiates to $-8$. Since there are many such numbers, and no canonical choice among them, $(-8)^{-1/3}$ is undefined. But $\frac{1}{\sqrt[3]{-8}}$ is defined since $\sqrt[3]{x}$ has a different definition: the unique real number that cubes to $-8$. – 2'5 9'2 Dec 10 '15 at 21:19
The relation $x^{1/n}=\sqrt[n]{x}$ is only valid for positive $x$. When you extend this the way you do to negative $x$, you are not doing what mathematicians do with such expressions. – 2'5 9'2 Dec 10 '15 at 21:20
This is because $e^{\ln{x}}\neq{x}$ when $x<0$ – Arbuja Dec 10 '15 at 22:04
For the first comment you must include the negative outputs when $x<0$. For example when you take ${x}^{x}$ for $x=-1/3,-3/3,-5/3$ and any $x=\frac{\text{odd integer}}{\text{odd integer}}$ the values are negative. Hence you should also use $-|x|^{x}$ when $x<0$. – Arbuja Dec 10 '15 at 22:12
I'm talking about the real numbers, not about complex number. For complex number you use the Complex logarithm which is $\text{Log}z$ not $\ln\left({x}\right)$. – Arbuja Dec 10 '15 at 22:30
@Arbuja It's pointless for us to discuss the details of your rational exponents and how they are calculated. As noted, you are using a definition for $(\text{negative real})^{\text{real}}$ that is different than the one I use (which is the one CAS's and others use). It's not that either of us is wrong, just that, imho, the meaning that my answer is based on is more standard than the meaning which yours is based on. – 2'5 9'2 Dec 10 '15 at 22:57
I believe your answer is much simpler and more professional. The OP will definitely understand what you are saying. – Arbuja Dec 10 '15 at 23:30

Graph of $y=x^x$ for $x<0$

3 Answers3