Infimum of $x^x$

Question

The question is to find the infimum of $$f(x)=x^x$$

This is the question I tried and I obtain the answer as $e^{-\frac1e}$ but I don't understand why did he define the function as $f\colon\mathbb R\to\mathbb R$ when $\color{blue}{\text{the domain of this function is}}$ $x>0$. I don't understand $\color{red}{\text{how it can be negative?}}$

Maybe I don't know the meaning of infimum or the greatest lower bound. I know it is different from minimum of function but in this case I don't understand. Please help !

Answer 1

$f$ is not $\mathbb R \to \mathbb R$, since $f(x)$ is not real for most negative $x$, so this is a bad question. That then leads you to trying to interpret the graph to work out what was actually intended.

Visually, the lowest point on the graph seems to be near $x=-\frac13$

If you try to interpret $\left(-\frac13\right)^{-1/3}$ as the reciprocal of the real cube root of $-\frac13$ then you get $f\left(-\frac13\right) = -{3}^{1/3} \approx -1.44225$.

Can you do better? Other values which might behave similarly include those of the form $-\frac ab$ where $a$ and $b$ are positive odd integers and $f\left(-\frac ab\right)= -\left(\frac ba\right)^{a/b}$. You need $b$ to be odd to give a real root and $a$ to be odd to give a negative result.

To make this as small as possible, you want to make $-y^{-y}=-\left(\frac1{y}\right)^y$ as negative as possible with $y$ positive and of suitable form $\frac ab$ where $a$ and $b$ are positive odd integers. Unconstrained on the positive reals that would be minimised by $y={e^{-1}}$ giving $-e^{e^{-1}}$. That $y$ is not of suitable form but it can be approached arbitrarily closely by rationals of the correct form and so $-e^{e^{-1}} \approx -1.444668$ is the desired answer.

For example $\frac{18089}{49171}$ is close to $e^{-1}$ and this would give $f\left(-\frac{18089}{49171}\right) = - \left(\frac{49171}{18089}\right) ^{18089/49171} \approx -1.444668$, which is extremely close to this infimum.

Answer 2

Okay this is a "machine generated" problem. And I don't think it is useful or fair question.

Grown up humans define $x^y$ as requiring that $x > 0$ and $x^y$ be defined for real (possibly irrational $y$) via the calculus definition[1].

Children humans define $x^y$ as requiring that $y$ be an integer and $x$ can be anything and $x^y = \underbrace{x*x*x*....*x}_{y\text{ times}}$.

And adolescent humans define $x^y$ as $y$ being a rational number written and $y=\frac mn$ in lowest terms ($n> 0$ but $m$ may be any integer) and $x^{\frac mn} =\sqrt[n]{x^m}$. $x$ can be any positive real but if $x< 0$ then we must have $n$ is odd and $x^y$ will flip from positive to negative whether $m$ is odd or even.

The adolescent human definition is rather naive and fairly useless and leads to confusion and problems. So "real" mathematicians use the grown-up human definition.

... But this "machine" used a combination of the adolescent human and the grown up human to have $x^x$ be the calculus real definition if $x > 0$, but if $x < 0$ then the adolescent domain only consists of rational numbers with odd denominators.

Now you are correct. For $f:\mathbb R^+ \to \mathbb R; f(x) = x^y$ the $\inf f(x) = e^{-\frac 1e}$ (when $x = \frac 1e$ then $f(x) =(\frac 1e)^{\frac 1e} = e^{-\frac 1e}$).

But if we allow negative rational with odd denominator values of $x$ into the domain as though we were adolescents then we can't have $\inf f(x) \ge 0$ because negative outputs do exist. SO the machine points at the $\inf f(x)$ if we allow negative values then the $\inf f(x) \approx -1.44467$. (This is $-e^{\frac 1e}$ by the way... and yes the value does not actually exist as the only negative values that do exist are the rationals with odd denominatiors-- but the $\inf f$ is a bound which need not be met... but... well, read the next paragraph....)

But I think this is an, at best, pointless question because that is a naive an problem riddled definition of exponents that grown-up mathematicians just don't use.

.... in my opinion.....

So, again in my opinion, I'd claim you are correct and the machine is wrong.... well, not wrong but rather severely missing the point of real analysis.

======

[1] There are two valid definitions of $b^x$.

One is $Ln:\mathbb R^+ \to \mathbb R$ via $Ln(x) = \int_1^x \frac 1t dt$. $Exp(x):\mathbb R \to \mathbb R^+$ via $Exp$ is the inverse function of $Ln$. That is $Exp(x) = Ln^{-1}(x) = y \iff Ln(y) = x$. And for $b > 0$ then $b^x = Exp(x\cdot Ln(b))$.

The other (far more intuitive but with many constructive and analytical drawbacks) is that $b^x$ is defined for $b > 0$ and $x\in \mathbb Q$ $b^x$ is defined the "adolescent" way above. But if $x \not \in \mathbb Q$ then if we take a sequence of rational $q_n$ so that $\lim q_n = x$ then $b^x$ is defined as $b^x = \lim b^{q_n}$.

Answer 3

It is possible to define $x^y$ even if $x$ is negative. This doesn't even require complex numbers. The function $x^2$ is perfectly well-defined even when $x<0$. In general, if $y$ is rational number $a/b$, where $b$ is odd, and $a$ and $b$ are coprime, then $$ x^y = \left(\sqrt[b]{x}\right)^a \, . $$ Note that $\sqrt[b]{x}=-\sqrt[b]{-x}$, and so $$ x^y= \left(-\sqrt[b]{-x}\right)^a=(-1)^a(\sqrt[b]{-x})^a=(-1)^a(-x)^y $$ In the case of $x=y$, this becomes $$ x^x=(-1)^a(-x)^x \, . $$ To find the infimum of $x^x$, we can restrict our attention to the case where $a$ is odd. This corresponds to the lower part of the dotted line on the graph. This is when $x^x=-(-x)^x$.

Consider the function $g(x)=-(-x)^x$. Using the fact that $g(x)=-\exp(x\log(-x))$ for $x<0$, we find $$ g'(x)=-e^{x\log(-x)}(\log(-x)+1) \, . $$ The minimum of $g$ occurs when $x=-1/e$, but notice that $x^x$ isn't even defined for this value. However, we can find values of $x$ which are arbitrarily close to $-1/e$ for which $x^x$ is defined. Hence, the infimum of $x^x$ is $$ -\left(\frac{1}{e}\right)^{-1/e} \approx -1.44 \, . $$

Answer 4

First you should know that the infimum does not need to belong to a set. If an infimum belongs to a set we call it a minimum. Since they defined $f: \mathbb{R}\to\mathbb{R}$ we need to check also for negative values.
Use $$log(f(x))=log(x^x)=xlog(x)$$ Now we determine the derivative which gives $$log(f(x))'=log(f(x))'*f'(x)=\frac{f'(x)}{f(x)}$$ But $$log(f(x))' = (xlog(x))'= log(x)+1$$

Now we can easily say $$\frac{f'(x)}{f(x)}=log(x)+1 \implies f'(x)=x^xlog(x)+x^x$$.

However this function is only well defined for $x>0$. If we take a look for $x=-y$ we find a problem. It is only defined for $(\frac{p}{q})^\frac{p}{q}$ for p negative and q odd and positive. Let's try for a negative value. We find for $y=-x$ that $$f'(y)=y^ylog(y)+y^y=f'(-x)=-x^{-x}log(-x)+-x^{-x}$$ Let $f'(y)=0$ then $-x^{-x}log(-x)=x^{-x} \implies -log(-x)=1$ By taking the exponent this has a zero for $x=-\frac{1}{e}$.
However not every outcome is real, so you could check that. In fact, if we write $x^x = e^{x\log(x)} = e^{x\log(x) + 2i\pi k}$; where each $2i\pi k$ represents another branch of the complex logarithm.

For your anwer we only want to look at since it have to be real numbers.

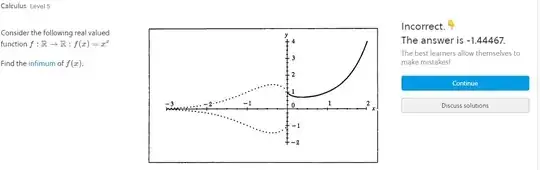
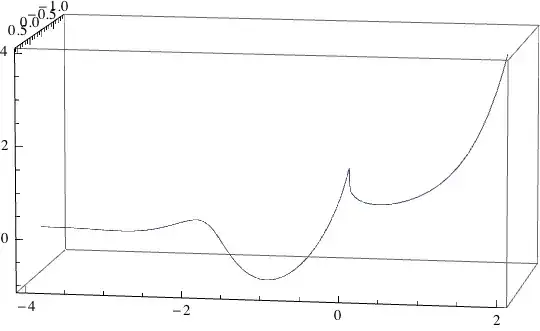This is the so called x-spindle. You can find more about this here.