Sanchez proposed the example of $\displaystyle\frac 1{1-x}=1+x+x^2+\cdots$ with $\,x\in\mathbb{R}\,$ that becomes $\displaystyle\frac 1{1-z}=1+z+z^2+\cdots$ with $\,z\in\mathbb{C}\,$. Note that this is not defined for $z=1$.
Practically this means that the computations over reals have to be replaced by the corresponding computations over complex values.
Let's start on the real axis near $x_0$ with the more general expansion :
$$f(x)=a_0+a_1(x-x_0)+a_2(x-x_0)^2+\cdots$$
To simplify a little analytic continuation is about getting the same expansion $$f(z)=a_0+a_1(z-z_0)+a_2(z-z_0)^2+\cdots$$ for complex numbers $z$ around a complex point $z_0$ and similar expansions $f(z)=b_0+b_1(z-z_1)+b_2(z-z_1)^2+\cdots\;$ around other points $z_1,\;z_2$ and so to cover as much as possible the complex plane.
Let's start for example with $z_0=x_0=0$ for the $\displaystyle\frac 1{1-z}$ function (with a unit radius convergence disk) followed by two other disks centered at the complex values $z_1$, $z_2$ (avoiding the pole at $z=1$) then we get this picture :
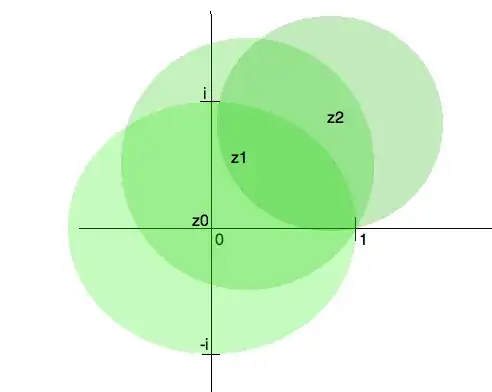
One advantage of complex analysis is that you'll see directly that for example $\displaystyle\frac 1{1+z^2}$ has a problem at $z=i$ and $z=-i$ (because the denominator vanishes !). Since $|i-0|=|-i-0|=1$ you may deduce that the convergence radius at $z_0=0$ of $\displaystyle\frac 1{1+z^2}=1-z^2+z^4-\cdots\,$ is $1$ (since the unit circle centered at $0$ will 'touch' the imaginary $i$ as well as $-i$ as illustrated above).
The complex points we need to avoid are named 'non removable singularities'. Near one of these points the smooth Taylor expansion will be replaced by a Laurent series :
$$f(z)=\cdots+\frac{a_{-2}}{(z-z_0)^2}+\frac{a_{-1}}{z-z_0}+a_0+a_1(z-z_0)+a_2(z-z_0)^2+\cdots$$
(with an infinite number of negative exponents in the case of an 'essential singularity')
Computing derivatives and integrals is done nearly as in the real case but with the second dimension we gained the possibility of integrating around circular contours (coming back to the starting point using a different path).
Let's compute $\int_C f(z)\;dz$ by evaluating its constituents : we have as in the real case $\displaystyle\int (z-z_0)^n\,dz=\frac {(z-z_0)^{n+1}}{n+1}$ except in the case $n=-1$ where we get the complex logarithm $\log(z-z_0)$. For $n\not =-1$ a counterclockwise contour integral will subtract two times the same value and be $0$ while for $n=-1$ the imaginary part will have gained and additional $2\pi\,i$ (see the picture from the last link).
This implies that the integral of the whole Laurent series over the contour will simply be $\ 2\pi\;i\;a_{-1}\ $ with $a_{-1}$ the famous 'residue' of $f$ at $z_0$.
Let's come to the zeta function that you probably saw defined as :
$$\zeta(z)=\sum_{n=1}^\infty \frac 1{n^z}$$
(or with $z$ written as $x$ real but at this point you should understand that it doesn't matter : the expression will be the same !)
The problem with this series is convergence : for real values of $z$ it will converge only for values larger than $1$ (from the 'integral test'). For complex values the problem is the same : it won't converge for $\Re(z)<1$ so that this series can't be used directly to find any zero of $\zeta$.
Fortunately a slight modification will allow to get convergence for $\Re(z)>0$ :
\begin{align}
\zeta(z)&=\frac 1{1^z}+\frac 1{2^z}+\frac 1{3^z}+\frac 1{4^z}+\frac 1{5^z}+\cdots\\
&=\frac 1{1^z}-\frac 1{2^z}+\frac 1{3^z}-\frac 1{4^z}+\frac 1{5^z}+\cdots+\frac 2{2^z}+\frac 2{4^z}+\cdots\\
&=\sum_{n=1}^\infty \frac {(-1)^{n-1}}{n^z}+\frac 2{2^z}\left(1+\frac 1{2^z}+\frac 1{3^z}\cdots\right)\\
\zeta(z)&=\sum_{n=1}^\infty \frac {(-1)^{n-1}}{n^z}+2^{1-z}\zeta(z)\\
\end{align}
Putting both $\zeta(z)$ at the left gives $\ \displaystyle\zeta(z)\left(1-2^{1-z}\right)=\sum_{n=1}^\infty \frac {(-1)^{n-1}}{n^z}\;$ and :
$$\zeta(z)=\frac 1{1-2^{1-z}}\sum_{n=1}^\infty \frac {(-1)^{n-1}}{n^z}$$
There is still a singularity at $z=1$ but we have now an alternate series that will converge on the real interval $(0,1)$ and in fact in the half-plane $\Re(z)>0$ (excluding only $z=1$) (proof). The (grossly schematized) analytic continuation process allows to go from the half-plane $\Re(z)>1$ to the half-plane $\Re(z)>0$ (minus $z=1$) and defines a unique function. We may for example use a convergence disk of radius $1$ centered at $z_3=2$ and then turn around $1$ using the $z_2$ from the picture and continue the process (remaining in the region $\Re(z)>0$).
Another formula for $\zeta$ that works well is obtained using Euler Maclaurin's expansion :
$$\zeta(z) \sim \sum_{k=1}^N \frac 1{k^z} \color{#bb0000}{+\frac 1{(z-1)\;N^{z-1}}}\\\color{#006600}{-\frac 1{2\;N^z}+\frac z{12\;N^{z+1}}-\frac{z(z+1)(z+2)}{720\;N^{z+3}}+\frac{z(z+1)(z+2)(z+3)(z+4)}{30240\;N^{z+5}}-\cdots}$$
The neat idea here (from Euler like most of the initial work about the real zeta function) is to :
- compute the first terms of the $\zeta$ series (more of them will mean higher precision and in fact we will need $2\,\pi\,N >\ |\Im(z)|$ so that $N=10$ is enough for imaginary parts under $60$)
- replace the remaining terms by the corresponding integral $\;\displaystyle\color{#bb0000}{\int_{N+1}^\infty \frac {dk}{k^z}}$
- add corrective terms to take into account the previous replacement of the sum by an integral. The numerical coefficients appearing here are the famous Bernoulli numbers divided by the corresponding factorial $\displaystyle\frac {B_n}{n!}$ with $B_{2n+1}=0$ for $n>0$.
It is interesting to observe that this formula remains valid for complex values and works too for negative real parts of $z$ (depending on the number of Bernoulli terms at the end).
Let's show too the Laurent series of $\zeta$ at $z=1$ with the simple pole at $1$ :
$$\zeta(z)=\frac 1{z-1}+\sum_{n=0}^\infty \frac{(-1)^n}{n!}\gamma_n\;(z-1)^n$$
with $\gamma_n$ the Stieltjes constants and $\gamma_0=0.5772156649\cdots$ the famous Euler constant.
The only complex zeros known have real part $\dfrac 12$ where the phase is simple so that the Z function $\;\displaystyle Z(t):=\zeta\left(\frac 12+it\right)\,e^{i\theta(t)}$ with $\,\theta$ $\displaystyle (t):=\Im\left(\log\Gamma\left(\frac 14 + \frac{i\,t}2\right)\right) - \frac{t}2\log(\pi)\,$ will be real and the zeros easy to find!
For faster evaluation see the different links from this thread or this discussion.
