(this is a kind of follow up to a discussion about partial sums starting with an introduction to $\zeta\,$)
Let's compare the two proposed methods to evaluate $\zeta\left(s\right)$ with $s=\frac 12+i\,t\ $ (Euler-Maclaurin may be applied everywhere, Riemann-Siegel may be used too if $\,\Re(s)\not =\frac 12$ but this is less documented) :
- Using Euler-Maclaurin you will need to compute the sum of at least the $\,N\approx \dfrac t{2\pi}\ $ first terms to get an accurate result (ignoring the 'cost' of a few Bernoulli terms and neglecting the remainder $R_{2v}$) from your expression :
$$\zeta(s)= \sum^{N}_{n=1} \frac{1}{n^{s}} + \frac{N^{1-s}}{s-1}-\frac 1{2\,N^s}+\frac{B_2}{2}sN^{-s-1} +\ldots + R_{2v}$$
To illustrate this let's add $3000$ terms ($\displaystyle 1,\,2^{-1/2-it},\,3^{-1/2-it},\cdots$) in the complex plane with the first term at the right at $1+0\,i$ and finishing near the middle at $0+0\,i\ $ because I choose $t$ to be the first value larger than $10000$ such that $\zeta\left(\frac 12+i\,t\right)=0\,$. This gave the picture :
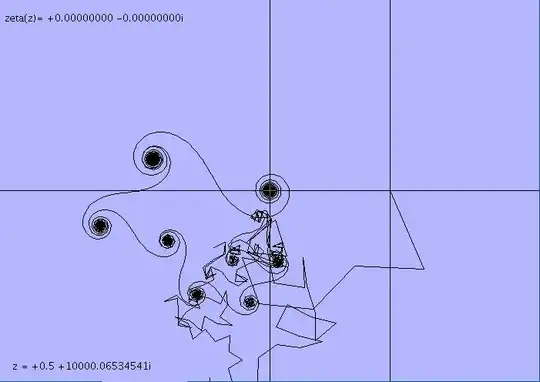
At this point let's apply the functional equation to the $N$ first terms of the series for $\zeta$ (consider every power term at $1-s$ instead of $s$ and multiply by $\gamma(1-s)$ as exposed at Wikipedia or at the bottom of this text) then we will get :
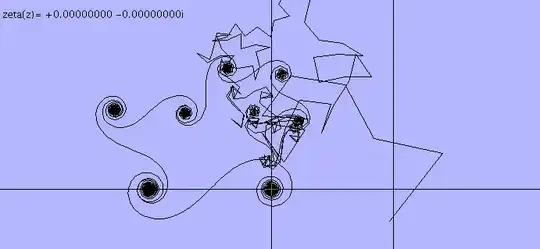
(in the simple case $\,\Re(s)=\frac 12\,$ this is merely a 'mirror effect' applied to the first picture : complex numbers are replaced by their conjugates and a global rotation depending smoothly of $t$ is applied)
Now let's superpose the second picture turned $180^\circ$ to the first one :
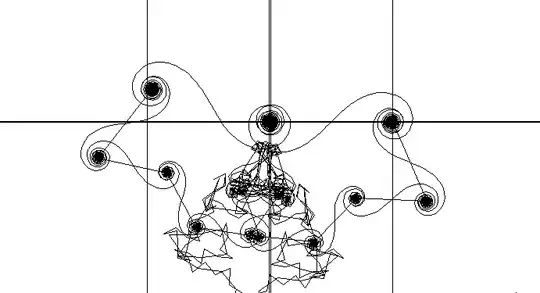
and observe the superposition of the first values (at the right on the first picture) to the final 'nodes' (at the left of the first picture).
- This is the whole point of the Riemann-Siegel formula :
from the $\,N\approx \dfrac {\Im(s)}{2\pi}\,$ terms needed to evaluate $\zeta(s)$ the first $[\sqrt{N}]$ terms provide half of the contribution while the remainder may be obtained with the $[\sqrt{N}]$ first terms terms of $\zeta(1-s)$ multiplied by $\,\gamma(1-s)$.
Replacing a sum over $N$ terms for Euler-Maclaurin by a sum over $[\sqrt{N}]$ terms is not uninteresting!
This may be done because of the functional equation : $$\zeta(s)=\gamma(1-s)\zeta(1-s)$$ with $\;\displaystyle\gamma(s):=\pi^{1/2-s}\frac{\Gamma(s/2)}{\Gamma((1-s)/2)}\;$ to give the "approximate functional equation" :
$$\zeta(s)=\sum_{n=1}^m\frac 1{n^s}+\gamma(1-s)\sum_{n=1}^m\frac 1{n^{1-s}} + R(s)$$
the price is a not so easy to evaluate remainder :
$$R(s)=\frac{\Gamma(1-s)}{2\pi i}\int_{C_m}\frac{(-x)^{s-1}e^{-mx}}{e^x-1}dx$$
(an approximation of this integral is needed for a precise evaluation)
The $\gamma$ notation used in the approximate functional equation is from Carl Erickson's very interesting and recommended article "
A Geometric Perspective on the Riemann Zeta Function's Partial Sums".
For a formal derivation of these expressions your may consult too Titchmarsh's book about zeta or the chap.7 of Edwards' excellent book with a direct link to similar formulas here.
The details of actual computations are clearly exposed by Takusagawa and Gourdon&Sebah (for more see Edwards' book or Pugh's thesis.


