(Updated)
As a complement to John M's proof (+1) I'll add some 'visual clarifications' (whatever this may mean...) about the behavior of the finite sum of $\zeta\;$ for a large but fixed ordinate $y\in\mathbb{R}^+$ :
$$\tag{1}S_y(N)=\sum_{k=1}^N\frac 1{k^{\,1/2+iy}}$$
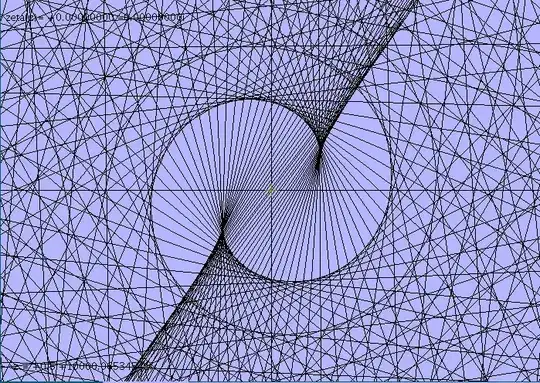
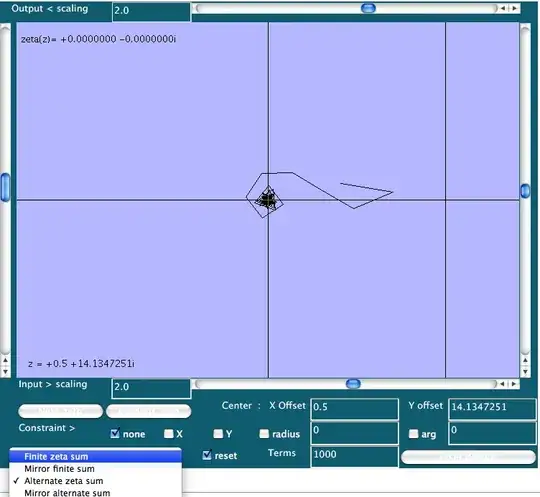
Let's suppose that $y$ is the first ordinate of a nontrivial zero larger than $10000$ and represent all the partial sums $\,S_y(N)$ for $\;N=1\cdots 3183=[y/\pi]\;$ in the complex plane :

The cross at the middle is at the origin ($z=0$) while '1' represents $z=S_y(1)=1$ and '2' $\;S_y(2)=1+\dfrac {2^{-iy}}{\sqrt{2}}$ and so on up to '3183' representing $\;S_y(3183)$ very near to $0$ again.
$$-$$
The picture shows figures looking like Cornu (or Euler) spirals. Let's justify this :
the sum $S_y(N)$ is obtained by addition of terms $\,\displaystyle \frac 1{k^{1/2+iy}}=\frac {e^{-iy\log(k)}}{\sqrt{k}}$.
The next term will thus be $\,\displaystyle \frac {e^{-iy\log(k+1)}}{\sqrt{k+1}}$.
Now for $k\gg 1$ the denominator will change only slightly while the change of phase of the numerator will be $\;\delta=-y\;(\log(k+1)-\log(k))=-y\,\log(1+1/k)\approx -\dfrac yk$.
$\delta\approx -\dfrac {y}k$ gives a special role to the values of $k$ such that $\dfrac yk\approx f\pi$ with $f$ integer :
- for $f=2m$ (i.e. $k=\left[ \frac y{2m\pi}\right]$) we have $\,\delta\approx -2m\pi\,$ : for values of $k$ near of $\left[ \frac y{2m\pi}\right]$ the terms have nearly the same phase and their addition will nearly give a straight line (see f=2, f=4, and so on on the picture)
- for $f=2m+1$ (i.e. $k=\left[ \frac y{(2m+1)\pi}\right]$) we have $\,\delta\approx -(2m+1)\pi\,$ : for values of $k$ near of $\left[ \frac y{(2m+1)\pi}\right]$ two consecutive terms nearly cancel each other and that's what is happening in the middle of the 'nodes' f=1, f=3, f=5 and so on.
Let's zoom the center of the final node $f=1$ :
The line nearly crossing the origin is obtained with the term $k=3183=\left[ y/\pi\right]$ while the line at its left and right came from $k=3182$ and $k=3181$ respectively. The value $S_y(3183)$ itself is far out of the picture (say $12$ or more times higher) while $S_y(3182)$ is far at the bottom on the other side. Taking the middle of these two values should bring us not too far from our target even if the different partial sums $S_y(N)$ don't really 'go down to $0$' ! (they merely turn around it)
All this explains (but doesn't prove) that an excellent approximation for $\zeta$ may be obtained (near the zeros at least) with the formula :
$$\zeta\left(\frac 12+iy\right)\approx -\frac 1{2\,[y/\pi]^{1/2+iy}}+\sum_{n=1}^{[y/ \pi]}\frac{1}{n^{1/2+iy}}$$
(numerically the absolute error appears majored by $\dfrac{2.5}{y^{3/2}}$ in the range $(10,10000)$, and probably for larger values, while the initial sum from the question was majored by $\dfrac{0.9}{y^{1/2}}$)
Now what happens when we continue adding terms after $\dfrac y{\pi}$ ? Well the difference of phase $\,\delta\,$ will become smaller than $\pi$ and we will turn round and round and obtain an ever growing ball of black wool :-) (illustration for $N=10^7$)
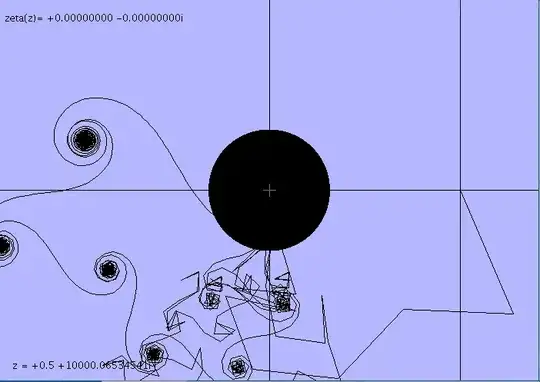
This discussion was rather qualitative and may be followed by these more general and precise expansions provided not only for $\,N=\left[\dfrac y{\pi}\right]\,$ terms but also for $\left[\dfrac y{e}\right]$ terms with $0<e<2\pi$.
But the story doesn't end here and Riemann himself found that you didn't need to compute the sum of $[y]$ terms (or $\left[\dfrac y{\pi}\right]$ or $\left[\dfrac y{2\pi}\right]$ or whatever) but that
$\left[\sqrt{\dfrac y{2\pi}}\right]$ terms were enough, at least if you accept some correction terms! (Riemann-Siegel formula)
and basic facts about Riemann $\zeta$ and the Euler Maclaurin formula.
As a fun alternative you may examine with care my first picture : notice that the distance from f=1 to f=3 is $1$, that the distance from f=3 to f=5 is $\dfrac 1{\sqrt{2}}$ and think 'Symmetry'!
All the pictures presented here were produced interactively using the (old) CSE applet that I created for Matthew R. Watkins (see the comments in case of problems).
Vitaliy Kaurov kindly provided nicer pictures using Mathematica.
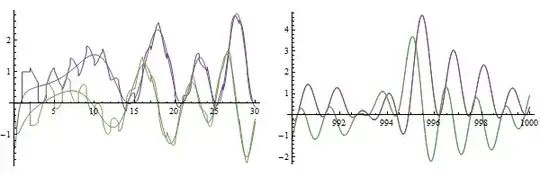
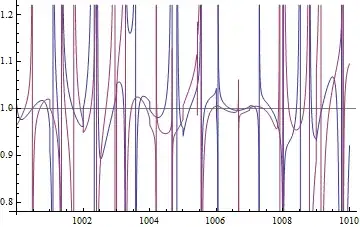



 (it is an applet from around 2001 so that modern browser support may be poor sorry...). There are no other reference than on this page (or the java source code) but I'll answer questions you could have about it.
(it is an applet from around 2001 so that modern browser support may be poor sorry...). There are no other reference than on this page (or the java source code) but I'll answer questions you could have about it.
x = 1/2; Plot[{Re[\!\( \*SubsuperscriptBox[\(\[Sum]\), \(n = 1\), \(y\)] \*FractionBox[\(1\), SuperscriptBox[\(n\), \(x + I\ y\)]]\)], Re[Zeta[x + I y]], Im[\!\( \*SubsuperscriptBox[\(\[Sum]\), \(n = 1\), \(y\)] \*FractionBox[\(1\), SuperscriptBox[\(n\), \(x + I\ y\)]]\)], Im[Zeta[x + I y]]}, {y, 0, 30}]– martin May 22 '14 at 14:06Let's add that a more accurate result should be obtained (I think) with your finite sum replaced by $$\sum_{n=1}^{\left[ y/\pi\right]}'\frac 1{n^{1/2+iy}}$$ with $[y/\pi]$ for round$(y/\pi)$ and ' meaning that we replace the last term of the sum by half of its value.
– Raymond Manzoni May 29 '14 at 00:39