More exactly the Riemann zeta function $\,\zeta\,$ is defined (and analytic) on the whole complex plane except for the simple pole at $1$.
This function was obtained by analytic continuation of the series $\;\displaystyle\mathcal{S}_s(\infty):=\sum_{k=1}^\infty\frac{1}{k^s}\;$ which is convergent only for $\,\Re(s)>1$.
You could obtain a convergent series for $\,\Re(s)>0\,$ by using $\;\displaystyle\zeta(s)=\frac 1{1-2^{1-s}}\sum_{k=1}^\infty \frac {(-1)^{k-1}}{k^s}$ but prefer to study the finite sums $\;\displaystyle\mathcal{S}_s(N):=\sum_{k=1}^N\frac{1}{k^s}\,$ for $\Re(s)=\frac 12\,$ which indeed gives fine results with an appropriate choice of $N$.
Concerning an analytic expression for the remainder you may use Marco's answer (+1) or following formula using the Hurwitz $\zeta$ function (we 'shift' the $N$ first terms) :$$\tag{0}R_s(N):=\zeta(s)-\mathcal{S}_s(N)=\sum_{k=0}^\infty\frac{1}{(N+1+k)^s}=\zeta(s,N+1)=\frac 1{\Gamma(s)}\int_0^\infty \frac{t^{s-1}e^{-N\,t}}{1-e^{-t}}\,dt$$
(strictly speaking this is valid only for $\,\Re(s)>1\,$ but the Hurwitz $\zeta$ function may be continued in the other half plane)
To answer shortly your question : the property doesn't evaporate for large $N$ since :
- We can use the finite sum of $N$ terms to approximate $\zeta(s)$ and will obtain acceptable results if $N$ is at least $\dfrac t{2\,\pi}$ with $t=\Im(s)$ (as you observed) and for any $N\gg 1$. Better precision may be obtained with an appropriate formula for the remainder. This is done for example using the Euler Maclaurin's expansion (near the end) or the expansion $(3)$ here.
- We may use an additional symmetry of $\zeta$ and get a precise estimation of $\zeta$ using only $\;\sqrt{\dfrac t{2\pi}}\;$ terms this is the Riemann-Siegel formula (the formula for the remainder is more complex).
$$-$$
An 'intuitive' exposition of these finite sums was given in this answser (please read it first since this is a kind of "follow up" : such an interesting story shouldn't end in a black spot!).
Vitaliy Kaurov kindly used Mathematica to produce nicer pictures of finite sums like this one :
(we start at the right in the complex plane at $\;1+0\,i=1^{-s}$, add $\,2^{-s}\,$ and so on...)
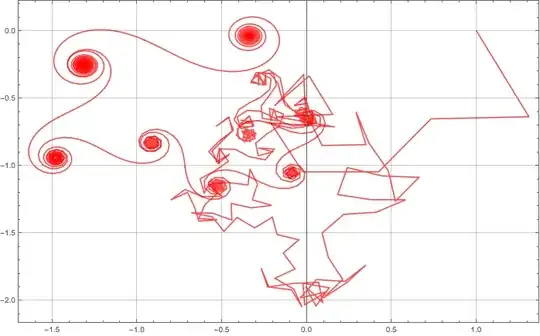
A result of the previous study was this first approximation :
$$\tag{1}\zeta\left(\frac 12+it\right)\approx -\frac 1{2\,[t/\pi]^{1/2+it}}+\sum_{n=1}^{[t/ \pi]}\frac{1}{n^{1/2+it}}$$
For $N=[t/ \pi]$ with $[x]$ the nearest integer (floor or ceil if used consistently should work too) this gives :
$$\tag{2}\zeta\left(\frac 12+it\right)\approx \mathcal{S}_{1/2+it}(N)-\frac 1{2\,N^{1/2+it}}$$
Now to obtain $(1)$ we didn't really require $s$ to be written as $s=\frac 12+it\,$ nor to be a zero of $\zeta$.
We could too take into account going from $\dfrac 1{\sqrt{N}}$ to $\dfrac 1{\sqrt{N+1}}$ (in the link) by replacing $\dfrac 1{2\,N^{1/2+it}}$ in $(2)$ by $\dfrac {1-1/(4N)}{2\,N^{1/2+it}}\;$ and add another term to $(2)$ but we may do better.
In the critical strip I obtained the much better expansion (not restricted to $\;\Re(s)=1/2)$ :
$$
\tag{3}\boxed{\displaystyle\zeta\left(s\right)=\mathcal{S}_s(N)-\frac {R_N(d)}{2\,N^s}}\quad
\text{for}\ N:=\left[\frac t{\pi}\right],\ d:=s-\pi\,N\,i$$
with
$$R_N(d):=1-\frac d{2\,N}+\frac{\pi\,i}{N^2}\frac{(3\,d+2)}{24}+\frac 1{N^3}\left(\frac{\pi^2}{48}(3\,d+4)+\frac{d\,(d+1)(d+2)}{24}\right)-\frac{\pi\,i}{N^4}\left(\frac{17\,\pi^2}{1152}(3\,d+6)+\frac{d^3+5\,d^2+7\,d+12/5}{24}\right)-
\frac 1{N^5}\left(\frac {31\,\pi^4}{2304}(3\,d+8)+\frac{17\,\pi^2}{384}\left(d^3+7\,d^2+44\,d/3+44/5\right)+\frac{d\,(d+1)(d+2)(d+3)(d+4)}{240}\right)+\frac {\pi\,i}{N^6}\left(\frac{691\,\pi^4}{46080}(3\,d+10)+\frac{31\,\pi^2}{576}(d^3+9\,d^2+25\,d+944/45)+\frac{17}{1920}(d^5+40\,d^4/3+65\,d^3+422\,d^2/3+128\,d+240/7)\right)+O\left(\frac {d^7}{N^7}\right)$$
There should be a nicer representation for the remainder $R_N(d)$ (the coefficient of the highest powers of $\pi$ in each parenthesis appears to be $\;\displaystyle\frac {2\,(1-4^l)}{3\;2^l\,l!}B_{2\,l}\frac{(i\,\pi)^{l-1}}{N^l}(3\,d+2\,(l-1))\;$ for example).
Further details and references about this expansion and the following one would be welcome
(I obtained them in july and august 2014 without a formal derivation...).
The previous results were obtained by stopping the sum at $\;N=\left[\dfrac {t}{\pi}\right]\,$ but what happens for $\;N=\left[\dfrac {t}{e}\right]$ ? It appears that we have to restrain the real denominator $e$ to $\,0<e<2\pi\,$ (the coefficients become infinite at $0$ and $\,2\pi$) and may conjecture that :
$$\tag{4}\boxed{\displaystyle\zeta\left(s\right)=\mathcal{S}_s(N)-\frac {\mathcal{R}_N(d)}{2\,N^s}}\quad
\text{for}\ N:=\left[\frac t{e}\right],\ d:=s-e\,N\,i$$
with for $\,c:=\cot(e/2)\,$ :
$$\mathcal{R}_N(d)=1+c\,i-\frac 1{2N}\left(d(1+c^2)-\frac {ec^2}{\sin(e)}\right)\\-\frac {i}{N^2}\left(\frac{d^2\,c}{4\sin(e/2)^2}+\dfrac{d\,(\sin(e)-e\,(2+\cos(e)))-\dfrac {2\,e}3(2+\cos(e))+e^2\dfrac{5+\cos(e)}{4\tan(e/2)}}{8\sin(e/2)^4}\right)\\+O\left(\frac {d^3}{N^3}\right)$$
There is probably a much simpler way to write this expansion but I didn't investigate this further yet... (the limit as $\;e\to \pi\,$ returns the three first terms of $(3)$ as it should)
