A question about the arctangent addition formula.

Question

In the arctangent formula, we have that:

$$\arctan{u}+\arctan{v}=\arctan\left(\frac{u+v}{1-uv}\right)$$

however, only for $uv<1$. My question is: where does this condition come from? The situation is obvious for $uv=1$, but why the inequality?

One of the possibilities I considered was as following: the arctangent addition formula is derived from the formula:

$$\tan\left(\alpha+\beta\right)=\frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}\tan{\beta}}.$$

Hence, if we put $u=\tan{\alpha}$ and $v=\tan{\beta}$ (which we do in order to obtain the arctangent addition formula from the one above), the condition that $uv<1$ would mean $\tan\alpha\tan\beta<1$, which, in turn, would imply (thought I am NOT sure about this), that $-\pi/2<\alpha+\beta<\pi/2$, i.e. that we have to stay in the same period of tangent.

However, even if the above were true, I still do not see why we have to stay in the same period of tangent for the formula for $\tan(\alpha+\beta)$ to hold. I would be thankful for a thorough explanation.

Answer 1

If $\arctan x=A,\arctan y=B;$ $\tan A=x,\tan B=y$

We know, $$\tan(A+B)=\frac{\tan A+\tan B}{1-\tan A\tan B}$$

So, $$\tan(A+B)=\frac{x+y}{1-xy}$$ $$\implies\arctan\left(\frac{x+y}{1-xy}\right)=n\pi+A+B=n\pi+\arctan x+\arctan y $$ where $n$ is any integer

As the principal value of $\arctan z$ lies $\in[-\frac\pi2,\frac\pi2], -\pi\le\arctan x+\arctan y\le\pi$

$(1)$ If $\frac\pi2<\arctan x+\arctan y\le\pi, \arctan\left(\frac{x+y}{1-xy}\right)=\arctan x+\arctan y-\pi$ to keep $\arctan\left(\frac{x+y}{1-xy}\right)\in[-\frac\pi2,\frac\pi2]$

Observe that $\arctan x+\arctan y>\frac\pi2\implies \arctan x,\arctan y>0\implies x,y>0 $

$\implies\arctan x>\frac\pi2-\arctan y$ $\implies x>\tan\left(\frac\pi2-\arctan y\right)=\cot \arctan y=\cot\left(\text{arccot}\frac1y\right)\implies x>\frac1y\implies xy>1$

$(2)$ If $-\pi\le\arctan x+\arctan y<-\frac\pi2, \arctan\left(\frac{x+y}{1-xy}\right)=\arctan x+\arctan y+\pi$

Observe that $\arctan x+\arctan y<-\frac\pi2\implies \arctan x,\arctan y<0\implies x,y<0 $

Let $x=-X^2,y=-Y^2$

$\implies \arctan(-X^2)+\arctan(-Y^2)<-\frac\pi2$ $\implies \arctan(-X^2)<-\frac\pi2-\arctan(-Y^2)$ $\implies -X^2<\tan\left(-\frac\pi2-\arctan(-Y^2)\right)=\cot\arctan(-Y^2)=\cot\left(\text{arccot}\frac{-1}{Y^2}\right) $

$\implies -X^2<\frac1{-Y^2}\implies X^2>\frac1{Y^2}\implies X^2Y^2>1\implies xy>1 $

$(3)$ If $-\frac\pi2\le \arctan x+\arctan y\le \frac\pi2, \arctan x+\arctan y=\arctan\left(\frac{x+y}{1-xy}\right)$

Answer 2

You are correct in that it is related to the period. Note however, that while the period is unimportant for the tan addition formula to hold, the arc tan functions are defined by restricting the range to$(\dfrac{-\pi}{2},\dfrac{\pi}{2})$ If $uv>1 $, $\arctan u +\arctan v$ is not in the range of the arctan function(principal branch). In that case $\arctan \dfrac{u+v}{1-uv}$ is not the sum of the arctan's, it is shifted by $\pi$, up or down. Note that $\tan(\arctan u +\arctan v)=\tan(\arctan \dfrac{u+v}{1-uv})$ regardless of $uv<1$.

Answer 3

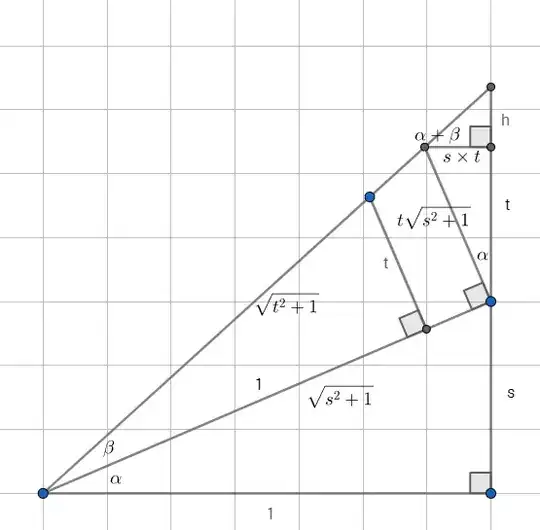
To explain why $\arctan(u) + \arctan(v) = \arctan(\frac{u+v}{1-uv})$ only if $uv < 1$, we need to recognise the obvious restriction of $$-\frac{\pi}{2} < \arctan(u) + \arctan(v) < \frac{\pi}{2}.$$

We'll consider three cases: $uv = 1$, $uv > 1$ and finally $uv < 1$.

If $uv = 1$ (the trivial case), $u$ and $v$ must have the same sign and $v = \frac{1}{u}$. From the identity $\arctan(u) + \arctan(\frac{1}{u}) = \pm\frac{\pi}{2}$:

$$\arctan(u) + \arctan(v) = \begin{cases} \frac{\pi}{2}, & \text{if $u, v > 0$}, \\[2ex] -\frac{\pi}{2}, & \text{if $u, v < 0$}. \\[2ex] \end{cases} $$

However, $\arctan(\frac{u+v}{1-uv})$ is obviously undefined when $uv=1$.

If $uv > 1$, both $u$ and $v$ must have the same sign again. Because of the behaviour of the inequality when dividing by a negative number, first consider the situation if $u, v > 0$: $$uv > 1 \implies v > \frac{1}{u},$$ $$\arctan(u) + \arctan(\frac{1}{u}) = \frac{\pi}{2},$$ $$\therefore \arctan(u) + \arctan(v) > \frac{\pi}{2}.$$

Similarly, if $u, v < 0$, $$uv > 1 \implies v < \frac{1}{u},$$ $$\arctan(u) + \arctan(\frac{1}{u}) = -\frac{\pi}{2},$$ $$\therefore \arctan(u) + \arctan(v) < -\frac{\pi}{2}.$$

Hence, we can see that whenever $uv > 1$, $\arctan(u) + \arctan(v) \notin (-\frac{\pi}{2}, \frac{\pi}{2})$.

If $uv < 1$, $u$ and $v$ may have different signs, but we can just consider $u > 0$, $u < 0$ and $u = 0$. If $u > 0$:

$$uv < 1 \implies v < \frac{1}{u},$$ $$\arctan(u) + \arctan(\frac{1}{u}) = \frac{\pi}{2},$$ $$\therefore \arctan(u) + \arctan(v) < \frac{\pi}{2}.$$

Similarly, if $u < 0$, $$uv < 1 \implies v > \frac{1}{u},$$ $$\arctan(u) + \arctan(\frac{1}{u}) = -\frac{\pi}{2},$$ $$\therefore \arctan(u) + \arctan(v) > -\frac{\pi}{2}.$$

If $u = 0$, consider the original equation $\arctan(u) + \arctan(v) = \arctan(\frac{u+v}{1-uv})$:

$$ \begin{align} LHS &= \arctan(0) + \arctan(v) \\ &= \arctan(v) \\ RHS &= \arctan(\frac{0+v}{1-0}) \\ &= \arctan(v) \\ &= LHS \end{align} $$

To summarise, we have shown that $$-\frac{\pi}{2} < \arctan(u) + \arctan(v) < \frac{\pi}{2}$$ is only true if $uv < 1$.

Bonus: To extend this to the arctangent subtraction formula, $$\arctan(u) - \arctan(v) = \arctan(u) + \arctan(-v)$$ $$\therefore u(-v) < 1 \implies uv > -1.$$

Answer 4

What is $\arctan{s}+\arctan{t}$? It is the addition of two angles: $\alpha+\beta$

Starting from the image we first calculate $h$:

$$\frac{h}{s\times t}=s+t+h$$

Therefore:

$$h=s\times t\frac{s+t}{1-s\times t}$$

And:

$$\tan{(\alpha+\beta)}=\frac{h}{s\times t}$$

$$\alpha+\beta=\arctan{s}+\arctan{t}=\arctan{\frac{s+t}{1-s\times t}}$$

Answer 5

A simpler explanation of why the identity $$\arctan u+\arctan v=\arctan\dfrac{u+v}{1-uv}$$ is valid if & only if $uv <1$.

By definition of the arctan function, as both sides have the same tangent, we only need to check under which condition $$-\frac\pi 2<\arctan u+\arctan v < \frac\pi2.$$ Let $\alpha=\arctan u$, $\beta=\arctan v$. A priori, $\alpha+\beta\in(-\pi,\pi)$, and on this interval, $$\alpha+\beta \in\Bigl(-\frac\pi 2,\frac\pi 2\Bigr)\iff \cos(\alpha+\beta)>0$$ Now $$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta = \cos\alpha\cos\beta(1-\tan\alpha\tan\beta)\\=\underbrace{\cos\alpha\cos\beta}_{>0}\,(1-uv)$$ has the sign of $1-uv$.