4

I have to convert a value from bark to Hertz.

I found the following formula to convert from Hz to bark:

$$\operatorname{Bark}(f)=13 \arctan(0.00076 f)+3.5 \arctan \left( \left( \frac{f}{7500} \right)^2 \right),$$ where $f$ is the frequency in Hz

Although i know that $\arctan(x)$ is the inverse of $\tan(x)$, i am unable to find the reversing function.

I am not good in mathematics. I also tried wolframalpha unsuccesfully

Mark Fantini
  • 5,523
Jan
  • 153
  • I'm not sure you'll find an explicit inverse, but it shouldn't be very difficult to numerically invert. – Ian Jul 12 '16 at 17:41
  • The function is monotonically increasing (for positive $f$) and continuous, and presumably $f$ is constrained to some known range (is it an audio frequency? then probably 0 to 20kHz or so), so you could perform a simple binary search to perform the inversion numerically. –  Jul 12 '16 at 17:43
  • Or just a look-up table.. A formula would be better.. and I cannot believe it does not exist.. But yes.. binary search is a good suggestion as it should be sufficient to approximate the value. Thank you – Jan Jul 12 '16 at 17:52
  • Maybe this can help http://math.stackexchange.com/questions/326334/a-question-about-the-arctangent-addition-formula – mathreadler Jul 12 '16 at 18:25

2 Answers2

4

The given function does not admit an elementary closed-form inverse. A (log-linear) plot of bark as a function of frequency (Hz) is shown below, over a frequency range of $10^{-1}$ Hz to $10^5$ Hz:

enter image description here

Note that the function is one-to-one. You can use the graph to obtain initial guesses for an iterative numeric method solution, such as a secant method, recursive bisection, or Newton's method (which might be overkill).

My suggestion is to use the formula to calculate a table, then reverse lookup the table to get an approximation, and use linear interpolation to refine the approximation, much like what one does with tables of common statistical distributions.

Here is a crude example in which I obtained inverse values for each half-integer value of bark from $b = 0.5$ to $b = 25$:

$$\begin{array}{|c|c|} \hline b & f \\ \hline 0.5 & 50.62 \\ \hline 1. & 101.35 \\ \hline 1.5 & 152.35 \\ \hline 2. & 203.77 \\ \hline 2.5 & 255.77 \\ \hline 3. & 308.52 \\ \hline 3.5 & 362.18 \\ \hline 4. & 416.93 \\ \hline 4.5 & 472.98 \\ \hline 5. & 530.54 \\ \hline 5.5 & 589.82 \\ \hline 6. & 651.1 \\ \hline 6.5 & 714.65 \\ \hline 7. & 780.77 \\ \hline 7.5 & 849.83 \\ \hline 8. & 922.21 \\ \hline 8.5 & 998.35 \\ \hline 9. & 1078.77 \\ \hline 9.5 & 1164.05 \\ \hline 10. & 1254.85 \\ \hline 10.5 & 1351.94 \\ \hline 11. & 1456.2 \\ \hline 11.5 & 1568.67 \\ \hline 12. & 1690.53 \\ \hline 12.5 & 1823.15 \\ \hline\end{array} \qquad \begin{array}{|c|c|} \hline b & f \\ \hline 13. & 1968.12 \\ \hline 13.5 & 2127.22 \\ \hline 14. & 2302.49 \\ \hline 14.5 & 2496.15 \\ \hline 15. & 2710.6 \\ \hline 15.5 & 2948.27 \\ \hline 16. & 3211.51 \\ \hline 16.5 & 3502.36 \\ \hline 17. & 3822.42 \\ \hline 17.5 & 4172.73 \\ \hline 18. & 4553.89 \\ \hline 18.5 & 4966.52 \\ \hline 19. & 5411.86 \\ \hline 19.5 & 5892.6 \\ \hline 20. & 6413.87 \\ \hline 20.5 & 6984.27 \\ \hline 21. & 7617.41 \\ \hline 21.5 & 8334.13 \\ \hline 22. & 9166.5 \\ \hline 22.5 & 10165.3 \\ \hline 23. & 11415.3 \\ \hline 23.5 & 13068.3 \\ \hline 24. & 15428.7 \\ \hline 24.5 & 19213.3 \\ \hline 25. & 26645.8 \\ \hline \end{array}$$

These are plotted in the figure below:

enter image description here

heropup
  • 135,869
  • Are you sure about this plot (and table)? If i put in the values in the formula i get different solutions – Jan Jul 18 '16 at 10:59
  • @Jan I am not sure why, but the original plots and tables must have been calculated incorrectly. I will edit it shortly. – heropup Jul 18 '16 at 14:40
1

You received a nice solution from @heropup.

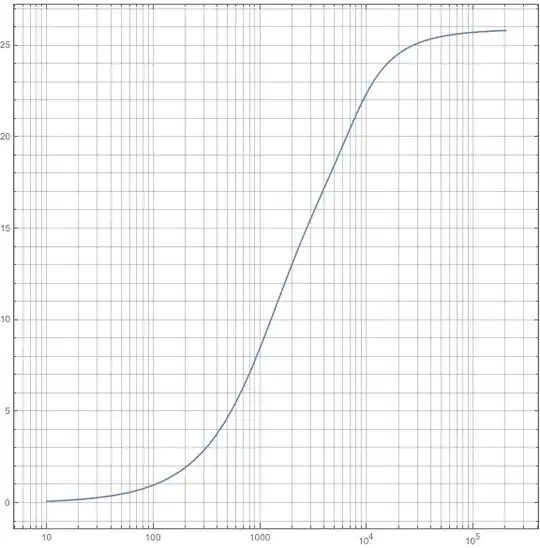
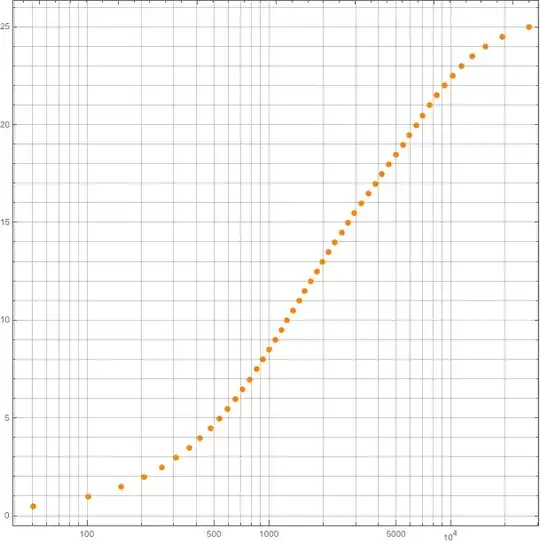
If you need to solve for $f$ (given in $kHz$) the equation $$b=13 \arctan(0.76 f)+3.5 \arctan \left( \frac{f^2}{57.25} \right)\tag 1$$ what I would suggest is to use the nice table given by @heropup and build a cubic spline for $\log(f)$ as a function of $b$. This need to be done only once and then to be applied. If you want to go further for more precise results, the result from the spline will give you the estimate $f_0$ from which Newton iterations could start. If the equation to solve is $$\Phi(f)=\alpha \arctan(\beta f)+\gamma \arctan \left( \frac{f^2}{\delta} \right)-b$$ you would get $$\Phi'(f)=\frac{\alpha \beta }{1+\beta ^2 f^2}+\frac{2 \gamma \delta f}{\delta ^2+f^4}$$ and the iterates would be given by $$f_{n+1}=f_n-\frac{\Phi(f_n)}{\Phi'(f_n)}$$

On the other side, searching the Web, I found this link in which you will notice that they propose for the inverse $$f=b \left(\frac{e^{0.219 b}}{352}+0.1\right)-0.032 e^{-0.15 (b-5)^2}\tag 2$$ which seems to be a "reasonable" approximation.

If we inject a value $f_1$ is $(1)$ in order to get $b$ and now use $(2)$ to compute $f_2$, for the range $0\leq f_1 \leq 16$, a simple linear regression gives $$f_1=0.958438 f_2$$ and the standard error for the coefficient is $0.005883$ $(R^2=0.998833)$.

Because of the curvature, we can do better and fit $f_1$ (the solution of $(1)$ as a cubic polynomial of $f_2$ (the estimate from $(2)$). This would give $$f_1=1.22179 f_2-0.0579613 f_2^2+0.00278296 f_2^3$$ corresponding to $(R^2=0.999875)$ (all three parameters being highly significant).

Edit

Back to the problem, using the formual you give in the post, I found a quite reasonable approximation $$b=\frac{27.3912 f-89.7986}{f+2268.8}$$ from which $f$ is simply obtained (at least for a first guess using Newton method). For this empirical expression, $R^2=0.99995$ and the parameters are very highly significant.

Claude Leibovici
  • 260,315