6

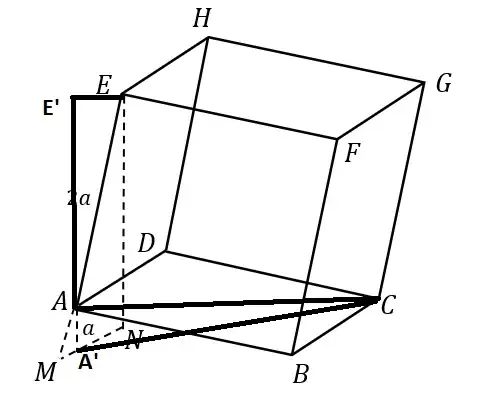
A cube $ABCD.EFGH$ has side length $2a$ cm. Point $A$ is lifted $a$ cm from the floor, point $C$ is still on the floor, point $B$ and point $D$ are on the same height from the floor. What is the height of point $E$ from the floor?

I'm sorry for my bad English, but I try to illustrate it as follows. 1

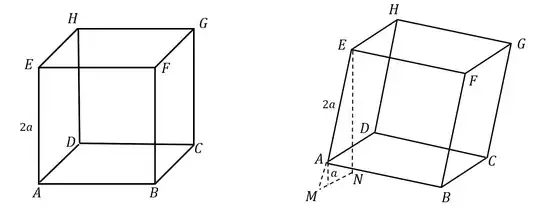
The left cube is the original one while the right side is the cube after we lifted the point $A$. In my mind, to find the height of point $E$ from the floor is to find the length of line $EN$. We can use Pythagorean theorem $EN^2=ME^2-MN^2$. But how to find the length of line $ME$ and $MN$?

RANGGAJAYA CIPTAWAN
  • 323
  • 1
    Note the similar triangles to determine MA – Moti Dec 16 '20 at 07:09
  • 1
    If you are interested in a similar problem which in fact involves rotation such that $B$ and $D$ are not at the same height (that question has $A$ on floor while $C$ lifts), you can go through my solution and other solutions here - https://math.stackexchange.com/questions/3880978/find-the-side-of-a-cube-having-a-vertex-is-on-a-flat-surface-and-three-vertices/3881654#3881654. – Math Lover Dec 16 '20 at 09:00

3 Answers3

4

enter image description here

As your pivot is point $C$ and points $B$ and $D$ are at the same height, the vertical edge AE will rotate by the same angle as the horizontal line $CA$.

(another way to think is $\triangle CAE$ rotating by angle $\theta$ in the same original plane)

If $\angle ACA' = \theta, \angle CAA' = 90^0 - \theta$.

where $A'$ is the vertical projection of point $A$ on the original surface.

Also $\angle CAE = 90^0$.

So, $\angle E'AE = 180^0 - (\angle CAE + \angle CAA') = 180^0 - (90^0 + 90^0 - \theta) = \theta$

Now $CA' = \sqrt{CA^2 - AA'^2} = \sqrt{{(2\sqrt2a)^2} - a^2} = a \sqrt 7$

So $\cos \theta = \frac{CA'}{CA} = \frac{a\sqrt7}{2a\sqrt2} = \frac{\sqrt7}{2\sqrt2}$

Now perpendicular distance of $E$ from the original horizontal plane

$= a + 2a \cos \theta \,$ ($\triangle AE'E \sim \triangle CA'A$)

$= A'A + AE' = a + 2a \frac{\sqrt7}{2\sqrt2} = a(1 + \sqrt{\frac{7}{2}})$

Math Lover
  • 51,819
1

You can also use similar triangles. Let $P$ be the point on $MN$ directly below $A$, and let $Q$ be the point of intersection of $EN$ and line $AC$. Since $\angle CAM$ is a right angle, we have that

$$\triangle CAP \sim \triangle AMP \sim \triangle EAQ$$

$CA \,$ is clearly $\, 2a \sqrt{2}\, $ so $\, PC = a\sqrt{7}\,.$ Then

$$\begin{align} \frac{AC}{PC} &= \frac{EA}{EQ} \\ \\ EQ &= \frac{EA \cdot PC}{AC} \\ \\ &= \frac{(2a)(a\sqrt{7})}{2a\sqrt{2}} \\ \\ &= a \sqrt {\frac{7}{2}} \\ \\ &= \frac{a}{2} \sqrt{14} \end{align}$$

and so the height of $E$ is

$$\begin{align} EQ + QN &= \frac{a}{2} \sqrt{14} + a \\ \\ &= \boxed{ a \left( \frac{\sqrt{14}}{2} + 1 \right) } \end{align}$$

A.J.
  • 3,892
0

Let $p = \angle ACA'$, $q = \angle ECA$ (in the original figure), where $A,C,A'$ are the same as in Math Lover's answer.

Then $\tan p = \frac{1}{\sqrt 7}, p = \tan^{-1} \frac{1}{\sqrt 7}$ and $\tan q = \frac{2}{2 \sqrt 2} = \frac{1}{\sqrt 2}, q = \tan^{-1} \frac{1}{\sqrt2}$. Now using the arctangent addition formula:

$$p + q = \tan^{-1} \frac{1/\sqrt7 + 1/\sqrt2}{1 - (1/\sqrt7)(1/\sqrt2)} = \tan^{-1} \frac{\sqrt{2} + \sqrt{7}}{\sqrt{14}-1} = \tan^{-1} \frac{\sqrt{2\cdot2\cdot7}+\sqrt{2\cdot7\cdot7}+\sqrt{2}+\sqrt{7}}{13} = \frac{1}{13} \left(8 \sqrt2 + 3 \sqrt7 \right).$$

So $\sin(p+q) = EN / EC \Rightarrow EN = 2\sqrt{3}a \sin(p+q)$. Now since $\sin(\tan^{-1} x) = \frac{x}{\sqrt{x^2+1}}$ (draw a triangle), then we have the monstrous task of simplifying this expression:

$$\sin(p+q) = \frac{(1/13) \left(8 \sqrt2 + 3 \sqrt7 \right)}{\sqrt{(1/169)(191+48\sqrt{14})+1}}$$

and after incorporating the $1$, denesting the square root, and dividing, I can confirm that this eventually gives $EN = a(1 + \sqrt{7/2})$.

Toby Mak
  • 16,827