Disclaimer: This is far from a completed answer. It contains
A) A proof of convergence that I felt necessary to establish at first (I didn't considered it as evident) providing as a side result, an understanding of the second term of the RHS part:
$$\pi \bigg( \text{ceil}\left(\frac ba+\frac 12\right) -1 \bigg) \tag{1}$$
(in which we have assumed $a>0$ WLOG).
B) The use of integral formula
$$\tan^{-1}\left(\tfrac{u}{t}\right)=\int_0^{\infty}\dfrac{e^{-xt}}{x}\sin(ux)dx\tag{2}$$
that looks promising but is still with the status "work in progress".
Part A:
Let
$$t_n:=\tan^{-1} (an+b)$$
Grouping symmetrical terms, one gets
$$t_{-n}+t_n= \tan^{-1}\dfrac{2b}{1-b^2+a^2n^2}+R_n\tag{3} $$
due to relationship (that can be understood with the following figure)
$$\tan^{-1}A+\tan^{-1}B=\tan^{-1}\dfrac{A+B}{1-AB}+R\tag{4}$$
where $R=-\pi,0,\pi$ according to the region in which $(A,B)$ is situated.
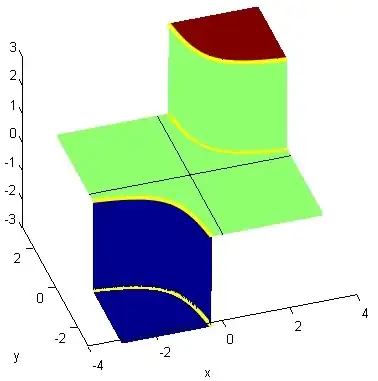
Fig. 1: Graphical representation of $R=\tan^{-1}A+\tan^{-1}B-\tan^{-1}\frac{A+B}{1-AB}$, with "plateaus" for $R=-\pi,0,\pi$. This is established in different references such as this one.
This "residual" $R_n$ is $0$ if
if $A$ and $B$ have the same sign with $AB<1$ or
if $A$ and $B$ haven't the same sign ; we are in this case here, when is $n$ large enough (as it is a proof of convergence, we can drop some terms without harm).
Otherwise said, $R_n$ becomes zero in (3) when $n$ is such that:
$$(an+b)(-an+b)<0 \ \iff \ b^2-n^2a^2<0$$
which amounts to say
$$n\ge n_0 \ \text{where} \ n_0:=\operatorname{ceil} \big|\tfrac{b}{a}\big|\tag{5}$$
In this way, it remains to sum up a series equivalent to the Riemann series $\sum 1/n^2$, therefore convergent.
Remark: Please note the close relationship between (5) and (1): (1) accounts for the "exceptional" terms $t_1+t_{-1}$, $t_2+t_{-2},...$ each one contributing with a $R_1=R_2=... = \pi$.
Remark: There is an exceptional term $t_0=\tan^{-1}(b)$ that will have to be taken into account later...
Part B: In order to "approach" expression
$$\tan^{-1} \left( \tan\frac{b\pi}{a} \cdot \coth \frac{\pi}{a} \right),\tag{6}$$
let us use formula (2) with $t=1$ and $u=an+b$: giving:
$$t_n:=\tan^{-1}(an+b)=\int_0^{\infty}\dfrac{e^{-x}}{x}\sin((an+b)x)dx$$
from which
$$I_n:=t_n+t_{-n}=2 \int_0^{\infty}\dfrac{e^{-x}}{x}\sin(bx)\cos(2anx)dx$$
otherwise expressed with the real part function $\Re$:
$$I_n=2 \int_0^{\infty}\dfrac{e^{-x}}{x}\sin(bx)\Re (e^{2iax})^n dx\tag{7}$$
Set apart the exceptional terms that we have considered just before, we need to compute the following sum (where $n_0$ has been defined in (5)):
$$S:=\sum_{n=n_0}^{\infty}I_n=2 \int_0^{\infty}\dfrac{e^{-x}}{x}\sin(bx)\Re \left(e^{2ian_0x}\dfrac{1}{1-e^{2iax}}\right)dx\tag{8}$$
$$S= \int_0^{\infty}\dfrac{e^{-x}}{x}\sin(bx) \left(\dfrac{\sin((2n_0-1)ax)}{\sin(ax)}\right)dx\tag{9}$$
It remains to match expressions (9) and (6)...
Please note that the parenthesized fraction in (9) can be expressed as $U_{2n_0-2}(\cos(ax))$ (Chebyshev polynomial of second kind), therefore doesn't need special care at the (removable) poles $x=\tfrac{k\pi}{a}$.
