Prove that $\int_0^\infty\frac1{x^x}\, dx<2$

Question

Prove that $$\int_0^\infty\frac1{x^x}\, dx<2.$$

_{Note: This inequality is rather tight. The integral approximates to $1.9955$.}

Integration by parts is out of the question. If we let $f(x)=\dfrac1{x^x}$ and $g'(x)=1$ then $f'(x)=-x^{-x}(\ln x + 1)$ by implicit differentiation and $g(x)=x$. The integral $\int f'(x)g(x)\, dx$ looks even harder to evaluate.

Expressing the left-hand side as a Frullani integral $$\int_0^\infty\frac{f(ax)-f(bx)}x\, dx=(f(0)-f(\infty))\ln\frac ba$$ means that $f(ax)-f(bx)=x^{1-x}$. However, I can't seem to find a continuous function $f$ that satisfies the functional equation. Is there such a function?

_{(For context, user371838's post below proves sophomore's dream which I also asked about originally.)}

Answer 1

$$\int_{0}^{+\infty}e^{-x\log x}\,dx = \underbrace{\int_{0}^{1}e^{-x\log x}\,dx}_{I_1}+\underbrace{\int_{1}^{+\infty}e^{-x\log x}\,dx}_{I_2} $$

$$ I_1=\sum_{n\geq 0}\frac{(-1)^n}{n!}\int_{0}^{1}x^n\left(\log x\right)^n\,dx = \sum_{n\geq 0}\frac{1}{(n+1)^{n+1}}=\sum_{n\geq 1}\frac{1}{n^n}\tag{A}$$

$$ I_2 = \int_{0}^{+\infty}e^{-(x+1)\log(x+1)}\,dx=\int_{0}^{+\infty}\frac{e^{-x}}{W(x)+1}\,dx\tag{B} $$ where $(A)$ gives $I_1\leq 1.292$ and high-order Padé approximants give $I_2\leq 0.705$.
It is a very tight inequality: I wonder if it can be proved in a more elementary way, maybe by writing the whole integral as $\int_{1}^{+\infty}e^{-x}g(W(x))\,dx$.

Answer 2

This approach is based on the intermediate inequalities, which follow from the series representations.

Using inequality $$x^{-x}\le1+(\sqrt[e]e -1)ex(2-ex)+ \frac{116-ex}{635} \sqrt{e x} (ex-1)^2,\quad\text{if}\quad x\in[0,1],\tag1$$

one can get $$I_1 \le \dfrac1e\int\limits_0^e (1 + (\sqrt[e]e - 1) (2 y - y^2) + \dfrac{116-y}{635} \sqrt y\, (y - 1)^2)\,\text dy,$$ $${\small I_1 \le 1 - e + \dfrac{e^2}3 + \sqrt e\left(\dfrac{232}{1905} - \dfrac{466 e}{3175} + \dfrac{236 e^2}{4445} - \dfrac{2 e^3}{5715}\right) + \dfrac{\sqrt[e]e (3e-e^2)}3 < 1.291733}\tag2$$ (see also Wolfram Alpha integration).

If $\;x\in[1,3],\;$ then $$\begin{align} &(2-x)\left(1+\dfrac1{120}(x-1)^6\right) + \dfrac1{12}(x-1)^3 (x^2-6x+11)\\[4pt] &+ \dfrac1{602910}(x-1)^8(470 +381(x-e) -270 (x-e)^2 +115(x-e)^3) -x^{-x} \le 0, \end{align}\tag3$$ $$\begin{align} &I_2 = \int\limits_1^3 x^{-x}\,\text dx \le \int\limits_0^2\bigg(1-y)\left(1+\dfrac1{120}y^6\right) + \dfrac1{12}y^3 (y^2-4y+6) + \dfrac1{602910}y^8\\[4pt] &\times\bigg(470 +381(y+1-e) -270 (y+1-e)^2 +115(y+1-e)^3\bigg)\bigg)\,\text dy = \bigg(\dfrac{y^9}{5426190}\\[4pt] &\times\left(\dfrac{345}4 y^3 - \dfrac{135(23e - 5)}{11} y^2 + \dfrac{27(62 - 50 e + 115 e^2)}{10} y + 696 - 186 e + 75 e^2 - 115 e^3\right) \\[4pt] & - y^8/960 + y^7/840 + y^6/72 - y^5/15 + y^4/8 - y^2/2 + y\bigg)\bigg|_0^2, \end{align}$$ $$I_2 \le \dfrac{2 (61687647 - 11159040 e + 4899840 e^2 - 809600 e^3)}{149220225} < 0.687550.\tag4$$

At last, $$I_3 = \int\limits_3^\infty x^{-x}\,\text dx = 3\int\limits_0^\infty (3+3y)^{-3-3y}\,\text dy = 3\int\limits_0^\infty3^{-3-3y}(1+y)^{-3-3y}\,\text dy$$ $$I_3 \le \dfrac19\int\limits_0^\infty \dfrac{27^{-y}}{(1+y)^3}\,\text dy = \dfrac{1-3\ln3\,(1 + 81\ln3\, \text{Ei}(-3\ln3))}{18} < 0.018865\tag5$$ (see also WA integration)

From $(2),(4),(5)$ should $$I=I_1+I_2+I_3 < 1.9982 <2.$$

On the other hand, $$I_1=\sum\limits_{n=1}^\infty \dfrac1{n^n}\le 1+\dfrac14+\dfrac1{27} +\dfrac1{256} + \dfrac1{3125}+\sum\limits_{n=6}^\infty\dfrac1{n^6},$$ $$I_1 \le 1+\dfrac14+\dfrac1{27} +\dfrac1{256} + \dfrac1{3125}+\dfrac{\pi^6}{945} < 1.291302,$$

$$\color{brown}{\mathbf{I< 1.291302 + 0.687550 + 0.018865 < 1.99772}}.$$

Answer 3

Remarks: Here is an alternative proof. I used the same bounds for this question Improper integral inequality including the golden ratio and the Sophomore's dream

---

We will use the following auxiliary results (Facts 1-2).

Fact 1: $x^{-x} \le \frac{3 - x}{x^2 - x + 2}$ for all $x \in [1, 2]$.
(RHS is the Pade $(1, 2)$ approximation of $x^{-x}$ at $x = 1$.)

Fact 2: $x^{-x} \le a^{-x} \mathrm{e}^{-x + a}$ for all $x, a > 0$.
(Proof: Taking logarithm on both sides, letting $u = \frac{a}{x} > 0$, it is equivalent to $\ln u \le u - 1$ which is true (easy).)

---

We have (Sophomore's dream) $$I_1 := \int_0^1 x^{-x} \mathrm{d} x = \sum_{n = 0}^\infty \frac{1}{(n + 1)^{n + 1}} \le 1 + \frac{1}{2^2} + \frac{1}{3^3} + \sum_{n=3}^\infty \frac{1}{4^{n + 1}} = \frac{2233}{1728}.$$

Using Fact 1, we have $$I_2 := \int_1^2 x^{-x}\mathrm{d} x \le \int_1^2 \frac{3 - x}{x^2 - x + 2}\mathrm{d} x = \frac{5}{\sqrt 7}\arctan \frac{\sqrt 7}{5} - \frac12\ln 2.$$

Using Fact 2, we have $$I_3 := \int_2^{5/2} x^{-x}\,\mathrm{d} x \le \int_2^{5/2} 2^{-x}\mathrm{e}^{-x + 2}\,\mathrm{d} x = \frac{2 - \sqrt{2\mathrm{e}^{-1}}}{8 + 8\ln 2},$$ and $$I_4 := \int_{5/2}^3 x^{-x}\,\mathrm{d} x \le \int_{5/2}^3 (5/2)^{-x}\mathrm{e}^{-x + 5/2}\,\mathrm{d} x = \frac{4\sqrt{10} - 8\sqrt{\mathrm{e}^{-1}}}{125\ln \frac{5}{2} + 125}, $$ and $$I_5 := \int_3^\infty x^{-x}\, \mathrm{d} x \le \int_3^\infty 3^{-x} \mathrm{e}^{-x + 3}\, \mathrm{d} x = \frac{1}{27\ln 3 + 27}.$$

Thus, we have \begin{align*} &\int_0^\infty x^{-x} \mathrm{d} x\\ =\, & I_1 + I_2 + I_3 + I_4 + I_5\\ \le\,& \frac{2233}{1728} + \frac{5}{\sqrt 7}\arctan \frac{\sqrt 7}{5} - \frac12\ln 2 + \frac{2 - \sqrt{2\mathrm{e}^{-1}}}{8 + 8\ln 2} + \frac{4\sqrt{10} - 8\sqrt{\mathrm{e}^{-1}}}{125\ln \frac{5}{2} + 125} + \frac{1}{27\ln 3 + 27}\\ <\,& 2. \end{align*}

We are done.

Answer 4

This is a well-known result but it is hard to Google it if you do not know what it is called. This, and a similar identity are known as the sophomore's dream and the proof is given here.

---

Important Note: This Proof is also present in Nahin’s Inside Interesting Integrals. However, this is how we learnt it in class as well.

---

We start with the identity $$x^{cx^a} = e^{cx^a\ln x} \tag 1$$ where $a$ and $c$ are constants. Using the power series expansion of the exponential $$e^y = 1 + y + \frac{y^2}{2!} + … $$ with $y = cx^a \ln x$ gives us: $$x^{cx^a} = 1+ cx^a\ln x + \frac{1}{2!}c^2x^{2a}\ln^2 x + \ldots $$ and so: $$\int_{0}^{1} x^{cx^a} \, dx = \int_{0}^{1}\, dx + c\int_{0}^1{} x^a \ln x\, dx + \frac{c^2}{2!} \int_{0}^{1} x^{2a}\ln^2 x\, dx + \ldots \tag 2$$

Now, to solve integrals of the form: $$I(m,n) = \int_{0}^{1} x^m\ln^n x \, dx $$ we simply make the substitution $u=-\ln x$, followed by another substitution $\chi = (m+1)u$ giving us: $$I(m,n) = \frac{(-1)^nn!}{(m+1)^{n+1}}$$

Hence, $(2)$ becomes $$\int_{0}^{1} x^{cx^a}\, dx = 1- \frac{c}{(a+1)^2} + \frac{c^2}{(2a+1)^3} - \frac{c}{(3a+1)^4}+\ldots$$

Now, if $c=-1$ and if $a=1$, it gives us: $$\int_{0}^{1} x^{-x}\, dx = 1 + \frac{1}{2^2}+\frac{1}{3^3}+\frac{1}{4^4}+\ldots$$

---

See also here.

Answer 5

This comment is not the proof, just wanted to share a quick idea. Lots of assumptions, because no proofs are provided.

Assume we know that $a(x)=\int_0^\infty\frac1{x^x}\, dx = a< \infty$. Then $a(x)/a$ is the valid probability density of some random variable, say $B$. Due to the Markov inequality we have $$ P(B>1)={1 \over a} \int_1^\infty\frac{1}{x^x}dx < {1 \over a} \int_0^\infty\frac{x}{x^x}dx, $$ wherefrom we get $$ \int_1^\infty\frac{1}{x^x}dx < \int_0^\infty\frac{1}{x^{x-1}}dx. $$

Assume the integral $\int_0^\infty\frac{1}{x^{x-1}}dx= \int_0^\infty a_1(x) dx=a_1<\infty$. Then $a_1(x)/a_1$ is the valid probability density of some random variable, say $B_1$. Again due to the Markov inequality we have $$ P(B_1>1)={1 \over a_1} \int_1^\infty\frac{1}{x^{x-1}}dx < {1 \over a_1} \int_0^\infty\frac{1}{x^{x-2}}dx. $$ Proceeding in the same way we get $$ \int_0^\infty\frac{1}{x^x}dx < \int_0^1\frac{1}{x^{x}}dx + \int_0^1\frac{1}{x^{x-1}}dx + \int_0^1\frac{1}{x^{x-2}}dx + \int_0^1\frac{1}{x^{x-3}}dx +\dots = \sum_{n=0}^\infty \int_0^1 {x^{n-x}}dx $$

Since Markov bound is very crude, not sure if this converges.

Answer 6

Big hint for the new year .

I simplify the answer of RiverLi we have for $x\in[1,3]$:

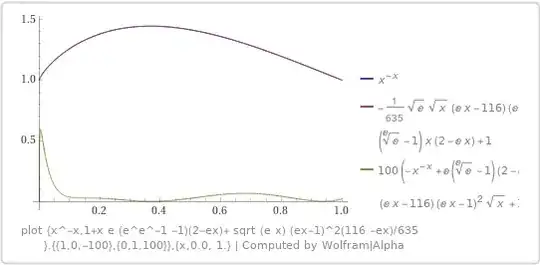
$$2^{1.449}x^{\frac{42}{100}}e^{-x^{1+\frac{42}{100}}}>x^{-x}$$

And using the Sophomore dream as RiverLi we have :

$$\int_{0}^{\infty}x^{-x}dx<\int_{1}^{3}2^{1.449}x^{\frac{42}{100}}e^{-x^{1+\frac{42}{100}}}dx+\int_{0}^{1}x^{-x}dx+\int_{3}^{\infty}3^{-x}e^{\left(-x+3\right)}dx<2$$

All the integral are easy and we are done !

---

---

---

Edit we have better in fact :

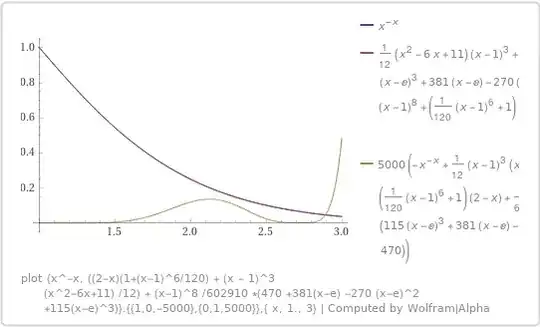
$$\int_{0}^{\infty}x^{-x}dx<\int_{1}^{5}ex^{\frac{12}{1000}+\frac{2}{5}}e^{-x^{\frac{12}{1000}+1+\frac{2}{5}}}dx+\int_{0}^{1}x^{-x}dx+\int_{5}^{\infty}x^{-x}dx$$

Or :

$$\int_{0}^{\infty}x^{-x}dx<\int_{1}^{5}ex^{\frac{12}{1000}+\frac{2}{5}}e^{-x^{\frac{12}{1000}+1+\frac{2}{5}}}dx+\int_{0}^{1}x^{-x}dx+\int_{5}^{\infty}5^{-x}dx$$

Where we have the inequality for $x\in[1,5]$ :

$$ex^{\frac{12}{1000}+\frac{2}{5}}e^{-x^{\frac{12}{1000}+1+\frac{2}{5}}}\geq x^{-x}\tag{I}$$

This inequality can be hadle with logarithm and derivative .

It leads us to using the Sophomore dream as RiverLi :

$$\int_{0}^{\infty}x^{-x}dx<e\cdot\frac{250}{353}\left(\frac{1}{e}-e^{-5^{1+\frac{103}{250}}}\right)+\frac{1}{3125\ln5}+\frac{27891287}{21600000}+\frac{1}{38800}<2$$

Or :

$$\int_{0}^{\infty}x^{-x}dx<\frac{250}{353}+\frac{1}{3125\ln5}+\frac{27891287}{21600000}+\frac{1}{38800}<2$$

I don't know if it could be shown by hand .

Some details :

$(I)$ proof :

We introduce the function :

$$f(x)=\ln\left(ex^{\frac{12}{1000}+\frac{2}{5}}e^{-x^{\frac{12}{1000}+1+\frac{2}{5}}}\right)-\ln\left(x^{-x}\right)$$

We have :

$$f'(x)=-\frac{353}{250}x^{\frac{103}{250}}+\frac{103}{250x}+1+\ln x$$

And :

$$f''(x)=\frac{-\left(36359x^{\frac{353}{250}}-62500x+25750\right)}{62500x^{2}}$$

The interesting part of the second dervative is :

$$g(x)=-\left(36359x^{\frac{353}{250}}-62500x+25750\right)$$

We have :

$$g'\left(\frac{61035156250000000\cdot2^{\frac{29}{103}}\cdot5^{\frac{87}{103}}}{164730217164529\cdot103^{\frac{44}{103}}\cdot353^{\frac{88}{103}}}\right)=0$$

Wich says for this value the function $g(x)$ have a maxima and :

$g(2.134...)=0$

Call $U=2.134...$

Now for $f'(x)$ we have $f(1)=0$ and $f'(x)$ is increasing before $x\in[1,U]$ and decreasing for $[U,5]$ with a zero at $V=3.66...$

Recalling that $f(1)=0,f(5)>0$ it shows the inequality $(I)$

For the integral :

$$\int_{1}^{5}ex^{\frac{12}{1000}+\frac{2}{5}}e^{-x^{\frac{12}{1000}+1+\frac{2}{5}}}dx$$

have the form $p'(x)r'(p(x))$ which is straightforward to integrating .

For the Sophomore Dream see RiverLi's answer .

Answer 7

I don't have a solution, but somehow interesting observation: $$\int_0^\infty x^{-x}dx=\int_0^1 x^{-x}dx+\int_1^2 x^{-x}dx+\int_2^3 x^{-x}dx+\dots=$$ $$\int_0^1 x^{-x}dx+\sum_{n=1}^\infty\int_0^1(x+n)^{-(x+n)}dx.$$ The second term $\int_0^1\sum_{n=1}^\infty(x+n)^{-(x+n)}dx$ looks like "double sophomore dream"; in $n$ as summation ($\sum_{n=1}^\infty n^{-n}$) and in $x$ as integral ($\int_0^1 x^{-x}dx$). But I don't know what to do with this next.

It would be nice to be able to find a tight bound, e.g., in terms of "sophomore dream" value. Note that $\left(\int_0^1x^{-x}dx\right)^{\int_0^1x^{-x}dx}=1.29128599^{-1.29128599}\approx 0.71885$.

Answer 8

Some toughts :

See https://www.isr-publications.com/jnsa/articles-1563-proofs-of-three-open-inequalities-with-power-exponential-functions

Using Vasc's lemma 7.1 we have :

$$a\left(\left((1-c)^{2}+ac(2-c)-ac(1-c)\ln a\right)\right)\geq x^{-x}$$

For $x\in[1,2]$ where $a=\frac{1}{x}$ and $c=x-1$

---

---

We have also :

$$\left(\frac{\left((1-c)^{2}+ac(2-c)-ac(1-c)\ln a\right)}{a^{b}}\right)^{\frac{1}{b}}\geq x^{-x}$$

For $x\in [0.5,1]$ and $c=2\left(1-x\right)$ , $b=2$ , $a=x$

---

---

And again :

$$a^{2}\left(\left((1-c)^{2}+ac(2-c)-ac(1-c)\ln a\right)\right)\geq x^{-x}$$

For $x\in[2,3]$ and $a=\frac{1}{x}$ and $c=x-2$

---

---

For other value we can be inspired by strong convexity/concavity of :

$$f\left(x\right)=x^{ax}$$

We have on $x\in(0,0.25]$ and $a=-3$:

$$\left(\frac{1}{f'\left(0.25\right)\left(x-0.25\right)+f\left(0.25\right)+\frac{\left(x-0.25\right)^{2}f''\left(0.25\right)}{2}}\right)^{\frac{1}{a}}\geq x^{-x}$$

Hope it helps .

Edit 22/04/2022 :

There is simpler we have on $(0.5,2)$ :

$$f\left(x\right)=\left(1+\frac{\left(x^{\frac{1}{2}}\left(\frac{x^{\frac{1}{2}}}{1-\left(x^{\frac{1}{2}}-1\right)^{2}}\right)-1\right)x^{\frac{1}{2}}}{2}\right)^{\left(-2\right)}-x^{-x}\ge0$$

So see https://www.wolframalpha.com/input?i=integral+%5Cleft%281%2B%5Cfrac%7B%5Cleft%28x%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D%5Cleft%28%5Cfrac%7Bx%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D%7D%7B1-%5Cleft%28x%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D-1%5Cright%29%5E%7B2%7D%7D%5Cright%29-1%5Cright%29x%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D%7D%7B2%7D%5Cright%29%5E%7B%5Cleft%28-2%5Cright%29%7D+at+0.5+to+2&assumption=%7B%22F%22%2C+%22Integral%22%2C+%22rangestart%22%7D+-%3E%220.5%22&assumption=%7B%22C%22%2C+%22integral%22%7D+-%3E+%7B%22Calculator%22%7D&assumption=%7B%22F%22%2C+%22Integral%22%2C+%22integrand%22%7D+-%3E%22%281%2B%28%28%28x%5E%28%28%281%29%2F%282%29%29%29%28%28%28x%5E%28%28%281%29%2F%282%29%29%29%29%2F%281-%28x%5E%28%28%281%29%2F%282%29%29%29-1%29%5E%282%29%29%29%29-1%29x%5E%28%28%281%29%2F%282%29%29%29%29%2F%282%29%29%29%5E%28%28-2%29%29%22&assumption=%7B%22F%22%2C+%22Integral%22%2C+%22rangeend%22%7D+-%3E%222%22

Edit 26/07/2022 :

We have the inequality for $0<x\leq 1$ :

$$\frac{\left(4-\frac{292}{100}x^{\frac{7}{10}}\left(x^{\frac{7}{10}}-1\right)\right)}{4+\frac{292}{100}x^{\frac{7}{10}}\left(x^{\frac{7}{10}}-1\right)}\geq x^{-x}$$