What is the actual loss in a feed line with high SWR?

Question

It is well-known that it is unwise to have standing waves on the feed line between one's antenna and one's transmitter, unless it is a very low-loss type (e.g. ladder line), because the transmitted signal is reflected multiple times through the feed line, incurring repeated losses.

How can I calculate the actual loss in dB, given that I know the SWR and the normal (with a matched source and load) loss of the feed line?

(I have already found an article which claims to derive a formula for the loss in the obvious fashion of summing the series of reflections. But I find it not all that clearly written for purposes of making use of the answer, and I also think that it would be good to have this question answered here on Amateur Radio SE.)

Answer 1

Assuming no tuner losses, and assuming uniform loss throughout the line (which isn't true in practice, yet can be a practical simplifying assumption, more below), feedline losses in decibels are:

$$ -10 \log \left(L { 1 - |\Gamma|^2 \over 1-L^2 \: |\Gamma|^2 }\right) $$

Where $L$ is the fraction of power transmitted by the feedline into a matched load:

$$ L := 10^{-\text{loss in decibels}/10} $$

and $\Gamma$ is the reflection coefficient:

$$ |\Gamma| := { \text{VSWR} -1 \over \text{VSWR} +1} $$

---

Derivation

Let's work an example and look at how it's derived.

Begin by calculating the loss of the feedline from the datasheet and the length. Let's say it's 0.46 dB per 100 feet, and 100 feet long, so feedline loss is 0.46 dB. Let's undecibel that and make it a ratio:

$$ L := 10^{-0.46/10} = 0.9 $$

Meaning, 90% of the power is transmitted, and the other 10% is absorbed by the feedline.

The math is easier if we express VSWR as a reflection coefficient $\Gamma$. It's a complex number but we don't care about the phase of the reflection (and we can't know it from just the VSWR anyway), so we'll calculate just the magnitude.

$$ |\Gamma| := { \text{VSWR} -1 \over \text{VSWR} +1} $$

Let's say for our example the VSWR is 2.35:1. That's a reflection coefficient of 0.4. This is a ratio of amplitude or voltage, so square it to obtain power: 16% of power is reflected, and the other 84% is accepted by the antenna.

And let's say forward power is 100 W. Furthermore, we'll assume the transmitter contains a tuner. When the tuner is adjusted so the transmitter sees a matched load, effective the tuner is inserting an impedance in the line which cancels the reflected wave, so the transmitter doesn't see any reflected power. Since the tuner (neglecting losses) has no resistive components to absorb any power and convert it to heat, this must mean all the reflected power that reaches the transmitter is reflected again back towards the antenna.

Now let's visualize what happens to that power as it reflects back and forth a few times.

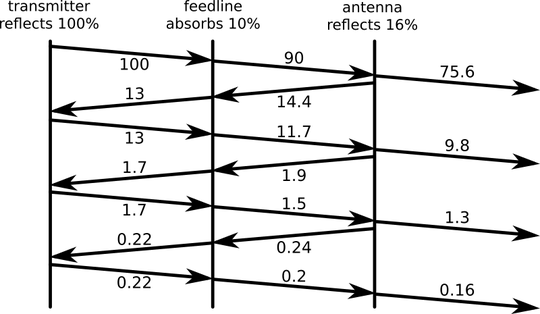
Sum all the power that was accepted by the antenna (75.6W + 9.8W + 1.3W + 0.16W + ...) to explain how much of that 100W was accepted by the antenna, and the rest was lost to the feedline. Shown in the diagram, a total of 86.8W makes it to the antenna. That means losses were:

$$ 10 \log\left(86.8 \over 100 \right) = 0.61\:\mathrm{dB} $$

Through more iterations we can obtain a more precise answer, but you can see that after a few reflections the powers have become small enough to be negligible.

Loss in decibels is calculated from the ratio of input power to output power, so let's calculate the fraction of input power that's accepted by the antenna.

Whatever the incident power at the antenna, $|\Gamma|^2$ of it is reflected, and $1-|\Gamma|^2$ of it is accepted. If we want to calculate the power accepted on a specific reflection, we need only find the incident power, and multiply it by $1-|\Gamma|^2$.

To calculate the incident power, we can count the number of trips though the feedline that have happened so far, and the number of times a reflection off the antenna has occurred so far. Each trip through the feedline reduces the power by a factor of $L$, and each reflection off the antenna by a factor of $|\Gamma|^2$.

For the first reflection, it's just one trip through the feedline and zero prior reflections.

$$ L^1 \: (|\Gamma|^2)^0 \: (1 - |\Gamma|^2) \\ \tag{accepted, 1st reflection}$$

On the second reflection, it's three trips through the feedline, and one prior reflection.

$$ L^3 \: (|\Gamma|^2)^1 \: (1 - |\Gamma|^2) \\ \tag{accepted, 2nd reflection}$$

On the third reflection, it's five trips through the feedline, and two prior reflections.

$$ L^5 \: (|\Gamma|^2)^2 \: (1 - |\Gamma|^2) \\ \tag{accepted, 3rd reflection}$$

A pattern emerges: the power accepted at each reflection is the same at the previous reflection, multiplied by

$$ L^2 \: |\Gamma|^2 $$

These summed together is the total power accepted:

$$ \sum_{n=0}^{\infty} L(1 - |\Gamma|^2) (L^2 \: |\Gamma|^2)^n $$

This is a geometric series, and can be simplified to

$$ \lim_{n \to \infty} L(1 - |\Gamma|^2) { 1-(L^2 \: |\Gamma|^2)^n \over 1-L^2 \: |\Gamma|^2 } $$

Because $L^2 \: |\Gamma|^2$ is less than 1, $(L^2 \: |\Gamma|^2)^n \to 0$ so the equation further simplifies to:

$$ L { 1 - |\Gamma|^2 \over 1-L^2 \: |\Gamma|^2 } $$

---

Limitations

A shortcoming of this model is real transmission lines don't have uniform loss.

Loss in a transmission line can be due to resistive loss, or dielectric loss. Resistive loss is proportional to the square of current, whereas dielectric loss is proportional to the square of voltage.

When the line is terminated in a mismatched load, standing waves form regions of high voltage alternating with regions of high current. The derivation above assumes losses occur uniformly in these regions, but in practice the resistive losses are more significant than the dielectric losses. Thus, the regions with high current have higher loss than the regions with high voltage.

For example, consider a short 50 ohm transmission line, say 1/10th of a wavelength long. This line could be terminated in either 5 ohms or 500 ohms, and in either case would experience an SWR of 10:1, and the method above would predict the same loss in either case. But in actuality, this line is so short the current and voltage anywhere along its length is more or less uniform.

In the case of the 5 ohm termination, current is going to be high, and the actual losses will be more than the equation predicts. With a 500 ohm termination, current will be low and actual losses will be less, possibly even less than the matched loss of the line. The higher the SWR, the higher the deviation from the equation.

If the line is electrically a multiple of half wavelengths long, there will be an equal number of high voltage and high current nodes. The effects cancel out, and actual losses are exactly as the equation predicts.

Also if the line is a large number of wavelengths long, there will be a large number of nodes so having one extra high voltage or high current node doesn't make a big difference overall.

The practical consequence is that the equation derived here is accurate, but not always precise. In a case such as a non-resonant multi-band antenna where the electrical length and load impedance are effectively random or unknown, this equation provides an accurate estimate. If the load impedance and electrical length are known, and especially if the electrical length is less than a couple wavelengths, it may be worthwhile to employ more precise methods.

Answer 2

I must admit I am probing the fringe of my understanding of transmission line theory at this point, but it is my understanding that the "number of passes" is one way of viewing what's going on, but it's sort of a clunky analogy for the integration of multiple reflections. Another way to think about it is that all of the reflections in the line sum together to increase the average current in the line.

Let's try a (probably overly) simplified thought experiment. Imagine a simple wire that is exactly one half wavelength long at an arbitrary frequency, and which is terminated via a perfectly matched resistive load to earth (essentially a short beverage antenna, for reference). If we were to send a single positive pulse (one half of one cycle) down the line, we can imagine that at some point in time, the current measured at the far end of the wire has not yet begun to rise, as the wave is still propagating toward it, but the current at the feedpoint has returned to something arbitrarily close to zero. The pulse is "half way" to the far end, so the current maximum is precisely in the center of the wire. A graph of the current along the length of the wire would look something like this.

The pulse is perfectly absorbed by the load, and there is zero reflection. At any point in time after the pulse has been absorbed, the current at any point on the wire would be zero.

Now imagine an imperfect termination. The pulse gets to the end of the wire and some part of it is reflected toward the feed point. We could snap that picture of the wave traveling forward toward the load, and shortly after snap a second picture of the reflected pulse, now attenuated due to partial absorption by the load, also centered up on the wire, but going the opposite direction (and inverted). If the system is ideal other than our mismatched load, the pulse would be perfectly reflected when it reached the feed point, and this ping-pong routine would continue until the pulse was fully absorbed. This is the "multiple passes", but I personally find it difficult to imagine this in the context of an actual antenna system.

Alternatively, we can imagine that we feed a continuous series of pulses in to this line, all of them positive, with an average power equal to 1 watt, and each new pulse beginning the instant we detect (through magic) that the current at the feed point from the previously generated pulse has reached zero. The first pulse travels to the end, and is partially reflected. A second pulse begins, and the two pass each other on the wire, summing together. The first pulse reaches the feedpoint end and is again reflected, just as the second pulse starts to reflect at the load end. At that instant, we start feeding a third pulse in.

As this continues, the amount of power reaching the load end at any instant rises steadily as numerous pulses with various phase angles sum together. At some point, the total power reaching the load is greater than the power being fed in. At this point the average power on the wire is greater than the 1 watt we are continuously feeding in.

Let's say that our load is absorbing exactly half the power on the wire, so for the first pulse, it dissipates 0.5 watts. Each partially reflected pulse increases the average power on the wire until, at some point, the power being absorbed by the load is equal to the power being fed in to the wire. At this point, we've reached equilibrium, but the average power (and thus average current) on the wire is greater than that of our input. The coax loss is derived not to the power fed in, but this average "circulating" power on the line.

The same principle dictates how a two wire feed line would behave, with each partially reflected cycle adding to the average circulating current. You must calculate the input power which would yield the same average power on the line with a perfectly terminated load, and then use that in the standard loss equation. If your load (along with standard conductive and dielectric losses) is absorbing 50% of the power that reaches it, you won't reach equilibrium with a 100w input until you have 200w circulating on the feed line. In reality it is not nearly so linear, but I must admit that the exact math to demonstrate the relationship is still a bit over my head at this point.

Incidentally, this is how an extremely high Q antenna like a magnetic loop can generate thousands of volts from only 100 watts input. The feed system permits very efficient coupling of power in to the antenna itself, but the resistive and radiative losses are all quite low, requiring a spectacularly high circulating power to achieve equilibrium. That's also why it is so essential that magnetic loops be as low loss as possible, to maximize the ratio of radiation resistance to all other losses.