Integrate $\int_0^{\pi/2} \frac{1}{1+\tan^\alpha{x}}\,\mathrm{d}x$

Question

Evaluate the integral $$\int_0^{\pi/2} \frac{1}{1+\tan^\alpha{x}}\,\mathrm{d}x$$

Answer 1

Use the fact that

$$\tan{\left (\frac{\pi}{2}-x\right)} = \frac{1}{\tan{x}}$$

i.e.,

$$\frac1{1+\tan^{\alpha}{x}} = 1-\frac{\tan^{\alpha}{x}}{1+\tan^{\alpha}{x}} = 1-\frac1{1+\frac1{\tan^{\alpha}{x}}} = 1-\frac1{1+\tan^{\alpha}{\left (\frac{\pi}{2}-x\right)}}$$

Therefore, if the sought-after integral is $I$, then

$$I = \frac{\pi}{2}-I$$

and...

Answer 2

The answer given by Gordon is very good for computing the integral. But it does not provide much why it works. The following figure might help with that

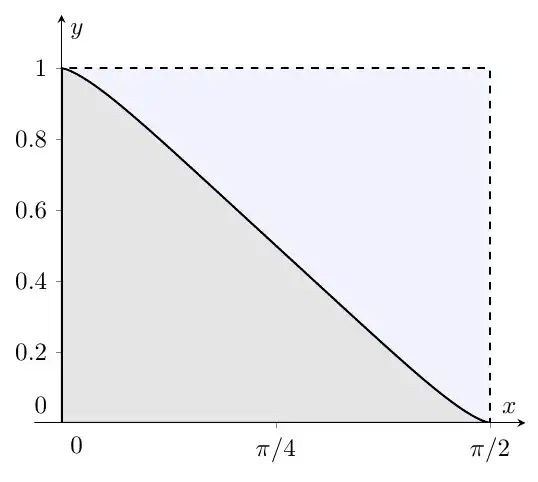
This is the integral for $\alpha=\sqrt{2}$. It looks as if the area under the function is exactly half of the dashed rectangle... A good guess is therefore $$ \int_0^{\pi/2} \frac{\mathrm{d}x}{1 + \tan(x)^\sqrt{2}} = \frac{1}{2}\left(\frac{\pi}{2}\right) $$ This striking symmetry can be shown true for any choice of $\alpha$, play around in geogebra or any ploting tool you fancy =)

The symmetry of such integrals is studied further in the paper Symmetri and Integration by Roger Nielsen Where it is shown that if $f(x) + f(a+b-x)$ is constant for all $x\in[a,b]$ - meaning it has this nice symmetric property.

Then the area can calculated as $$ \int_a^b f(x) \mathrm{d}x = \frac{f(a)+f(b)}{2}(b-a) = f\left(\frac{a+b}{2}\right)(b-a)\,. $$ I will leave it to you to check that $f(x)+f(a+b-x)$ is constant.

Alternatively the integral can also be computed as follows \begin{align*} \int_0^{\pi/2} \frac{\mathrm{d}\theta}{(1 + (\tan \theta)^b} = \int_0^\infty \frac{\mathrm{d}x}{(1+x^2)(1+x^b)} = \frac{1}{2} \int_0^\infty \frac{\mathrm{d}x}{1 + x^2} = \frac{\pi}{4} \end{align*} Where the substitution $u \mapsto \tan \theta$ was used and that $$ \int_0^\infty \frac{R(x)}{x^b+1}\mathrm{d}x = \frac{1}{2} \int_0^\infty R(x)\,\mathrm{d}x $$ Given that $R(x) = R(1/x)/x^2$, again check that this holds for $1/(1+x^2)$. A proof of the latter can be found on page $27$ here, section 1.9. More directly one has by the same methods \begin{align*} \int_0^\infty \frac{\mathrm{d}x}{(1+x^2)(1+x^b)} & = \int_0^1 \frac{\mathrm{d}x}{(1+x^2)(1+x^b)} + \int_1^\infty \frac{\mathrm{d}x}{(1+x^2)(1+x^b)} \\ & = \int_0^1 \frac{1}{(1+x^2)(1+x^b)} + \frac{x^b}{(1+x^2)(1+x^b)} \mathrm{d}x \\ & = \int_0^1 \frac{\mathrm{d}x}{1+x^2} = \frac{1}{2} \int_0^\infty \frac{\mathrm{d}x}{1+x^2} = \frac{\pi}{4} \end{align*} Where the substitution $x \mapsto 1/x$ was used in the last integral. These theorems and ideas are not the simplest way to attack the problem. But it might give you some broader insight further down the road.

Answer 3

The integral can be solved by using the fact that $\tan\left(\dfrac{\pi}{2}-x\right)=\dfrac{1}{\tan x}$ and $$ \int_a^b f(x)\;dx=\int_a^b f(a+b-x)\;dx. $$ Let $$ I(\alpha)=\int_0^{\frac{\Large\pi}{2}} \frac{dx}{1+\tan^\alpha x}, $$ then $$ \begin{align} I(\alpha)&=\int_0^{\frac{\Large\pi}{2}} \frac{dx}{1+\tan^\alpha\left(\frac{\pi}{2}+0-x\right)}\\ &=\int_0^{\frac{\Large\pi}{2}} \frac{dx}{1+\dfrac{1}{\tan^\alpha x}}\\ &=\int_0^{\frac{\Large\pi}{2}} \frac{\tan^\alpha x}{1+\tan^\alpha x}dx. \end{align} $$ Adding the two $I(\alpha)$'s yields $$ \begin{align} 2I(\alpha)&=\int_0^{\frac{\Large\pi}{2}} \frac{1}{1+\tan^\alpha x}dx+\int_0^{\frac{\Large\pi}{2}} \frac{\tan^\alpha x} {1+\tan^\alpha x}dx\\ &=\int_0^{\frac{\Large\pi}{2}}\;dx\\ &=\frac{\pi}{2}\\ I(\alpha)&=\large\color{blue}{\frac{\pi}{4}}. \end{align} $$

---

P.S.

I did NOT copy Ron Gordon's answer since this answer is taken from the similar problem that I posted on Brilliant.org - Trigonometric Integral of The Year. A similar problem can also be found on Mathworld Wolfram - Definite Integral.

Answer 4

Set $I(\alpha):=\int_0^{\pi/2} f(\alpha,x)dx$ where $f(\alpha,x):\mathbb{R}\times (0,\pi/2)\to \mathbb{R}$ is defined as $f(\alpha,x):=\frac{1}{1+\tan^\alpha(x)}$.

Since both $\frac{d}{d\alpha}f(\alpha,x)=-\frac{\tan^\alpha(x)\log(\tan(x))}{(1+\tan^\alpha(x))^2}$ and $f(\alpha,x)$ are continuous on $(0,\pi/2)\to \mathbb{R}$ we can apply the Leibniz integral rule obtaining

$$I'(\alpha)=\frac{d}{d\alpha}\int_0^{\pi/2}f(\alpha,x)\,dx=\int_0^{\pi/2}\frac{d}{d\alpha}f(\alpha,x)\,dx=0$$ since $\frac{d}{d\alpha}f(\alpha,\frac{\pi}{4}+x)=\frac{d}{d\alpha}f(\alpha,\frac{\pi}{4}-x)$ for $x\in[0,\frac{\pi}{4})$.

Hence $I(\alpha)$ is constant on $\mathbb{R}$ and $$I(\alpha)=I(0)=\int_0^{\pi/2}\frac{dx}{1+1}=\color{red}{\frac{\pi}{4}}.$$

Answer 5

Well, this problem has a nice symmetry. The integral can be rewritten as, $$ I=\int_{0}^{\pi/2}\frac{\cos^{\alpha}(x)}{\sin^{\alpha}(x)+\cos^{\alpha}(x)} dx \tag{1}$$ By the property of definite integrals this Integral is same as, $$\int_{0}^{\pi/2}\frac{\cos^{\alpha}(\frac{\pi}{2}-x)}{\sin^{\alpha}(\frac{\pi}{2}-x)+\cos^{\alpha}(\frac{\pi}{2}-x)} dx$$ $$\int_{0}^{\pi/2}\frac{\sin^{\alpha}(x)}{\sin^{\alpha}(x)+\cos^{\alpha}(x)} dx \tag{2}$$ Adding $1,2$ gives $$ 2I=\int_{0}^{\frac{\pi}{2}} dx$$ $$ 2I=\frac{\pi}{2}$$ $$\boxed{I=\frac{\pi}{4}}$$